Предмет: Алгебра,
автор: jislwncn
ПРОШУ СРОЧНО. ДАЮ 50 БАЛОВ
Приложения:
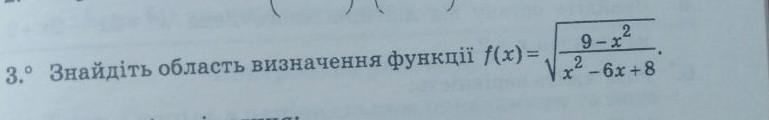
Ответы
Автор ответа:
0
Щоб знайти область визначення функції, ми маємо врахувати обмеження на значення змінних, які можуть приймати вирази у знаменнику функції.
У даному випадку, знаменник має вигляд x^2 - 6x + 8. Щоб визначити область визначення, ми повинні врахувати, коли цей знаменник не дорівнює нулю, оскільки ділення на нуль не визначено.
Розкладемо знаменник на множники:
x^2 - 6x + 8 = (x - 2)(x - 4)
Тепер, знайдемо значення x, при яких знаменник не дорівнює нулю. Це будуть значення, для яких (x - 2) і (x - 4) не рівні нулю одночасно.
(x - 2) ≠ 0 або (x - 4) ≠ 0
Розв'яжемо кожне з цих рівнянь:
(x - 2) ≠ 0
x ≠ 2
(x - 4) ≠ 0
x ≠ 4
Таким чином, область визначення функції буде будь-яке число, крім x = 2 та x = 4. У математичній нотації, область визначення можна записати як (-∞, 2) U (2, 4) U (4, +∞).
У даному випадку, знаменник має вигляд x^2 - 6x + 8. Щоб визначити область визначення, ми повинні врахувати, коли цей знаменник не дорівнює нулю, оскільки ділення на нуль не визначено.
Розкладемо знаменник на множники:
x^2 - 6x + 8 = (x - 2)(x - 4)
Тепер, знайдемо значення x, при яких знаменник не дорівнює нулю. Це будуть значення, для яких (x - 2) і (x - 4) не рівні нулю одночасно.
(x - 2) ≠ 0 або (x - 4) ≠ 0
Розв'яжемо кожне з цих рівнянь:
(x - 2) ≠ 0
x ≠ 2
(x - 4) ≠ 0
x ≠ 4
Таким чином, область визначення функції буде будь-яке число, крім x = 2 та x = 4. У математичній нотації, область визначення можна записати як (-∞, 2) U (2, 4) U (4, +∞).
Интересные вопросы
Предмет: Физика,
автор: ilovecatsssss
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: p944t8t9c4
Предмет: Математика,
автор: nastya03040
Предмет: География,
автор: anutkaorechva0448