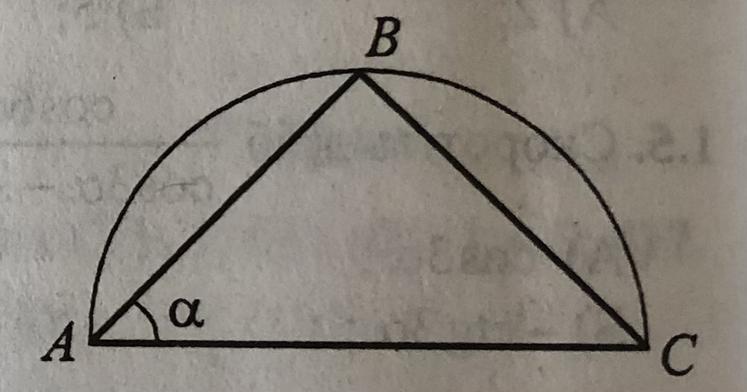
Чому дорівнює периметр трикутника, зображеного на рисунку, вписаного в півколо, радіус якого R, якщо a=45?

Ответ:

2R(1 + √2).

Объяснение:

1. По условию ∆ АВС вписан в окружность радиуса R, отрезок АС = 2R - диаметр окружности (т.к. в условии указано, что изображена половина этой окружности).

2. ∠ АВС вписанный, опирающийся на диаметр, тогда по.теореме ∠ АВС = 90°.

3. В ∆ ABC ∠ АВС = 90°, ∠ ВAС = 45°, тогда по теореме о сумме углов треугольника

∠ ВСА = 180° - (90° + 45°) = 45°,

∆ АВС - прямоугольный равнобедренный

4. Пусть АВ = ВС = х, по теореме Пифагора

х² + х² = (2R)²

2x² = 4R²

x² = 2R²

x > 0, x = √(2R²) = R√2.

3. P = AC + 2•AB = 2R + 2•R√2 = 2R(1 + √2).