Вычислите площадь фигуры, ограниченной линиями. y=x^2+1 и y=3-x
Сделайте пожалуйста на листочке ❤️

Ответ:       4.5   кв.ед.

Пошаговое объяснение:

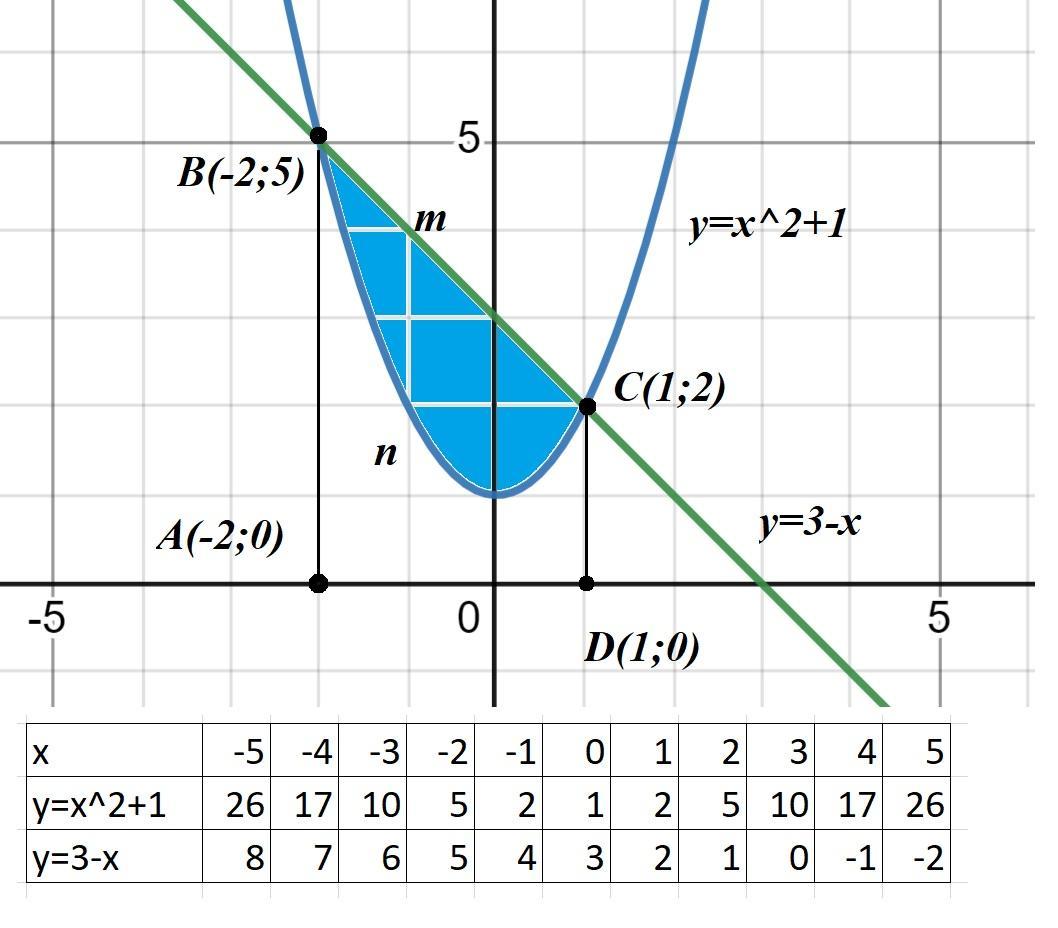
Строим графики функций y=x^2+1;   y=3-x.

Найдем абсциссы точек пересечения графиков

x^2+1 = 3-x.

x^2+x-2=0.

x1=a=-2;  x2=b=1.

Искомая площадь равна разности площадей двух криволинейных трапеций, опирающихся на отрезок [-2;1].

S=s(ABmCD) - s(ABnCD);

По формуле Ньютона-Лейбница s=∫ₐᵇf(x)dx=F(x)|ₐᵇ = F(b)-F(a)=>

S=∫₋₂¹(3-x)dx - ∫₋₂¹(x²+1)dx = 10,5 - 6 = 4.5   кв.ед.

1)  ∫₋₂¹(3-x)dx = ∫₋₂¹3dx - ∫₋₂¹(x)dx = 3(x)|₋₂¹ - 1/2(x²)|₋₂¹ =

= 3(1-(-2)) - 1/2(1²-(-2)²) = 3*3 - 1/2*(1-4) = 9-(-1.5)=10.5 кв.ед.

2)   ∫₋₂¹(x²+1)dx = ∫₋₂¹x²dx + ∫₋₂¹(1)dx = 1/3(x³)|₋₂¹ + x|₋₂¹ =

= 1/3(1³-(-2)³) + (1-(-2)) = 1/3(1+8) + 3 = 3+3 = 6 кв.ед.