Предмет: Алгебра, автор: yuimuii9411

Помогите плиз с Уравнением

Приложения:

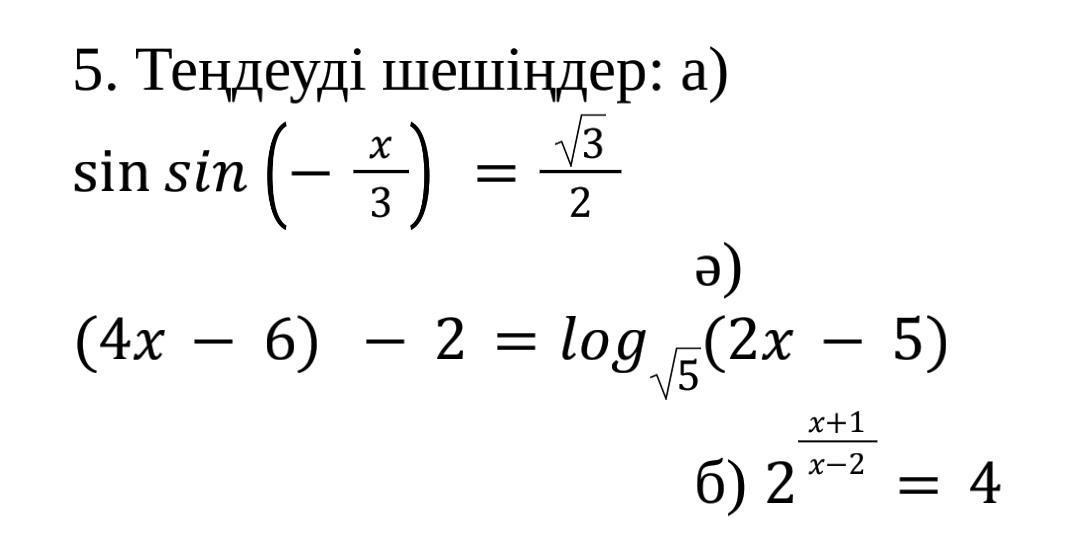
Ответы

Автор ответа: mathkot

Ответ:

а) Уравнение не имеет решение; $\boxed{ x \in \varnothing}$

б) Уравнение не имеет решение; $\boxed{ x \in \varnothing}$

в) Корень равен 5; $\boldsymbol{\boxed{x =5}}$

Примечание:

Все уравнения решаются на множестве действительных чисел

Объяснение:

а)

$\sin \sin \bigg(-\dfrac{x}{3} \bigg) = \dfrac{\sqrt{3} }{2}$

$\sin \bigg(-\dfrac{x}{3} \bigg) = (-1)^{k} \arcsin \bigg( \dfrac{\sqrt{3} }{2} \bigg) + \pi k, k \in \mathbb Z$

$\sin \bigg(-\dfrac{x}{3} \bigg) = (-1)^{k} \cdot \dfrac{\pi}{3} + \pi k, k \in \mathbb Z$

По свойствам функции синус область её значений принадлежит промежутку [-1;1], следовательно $\sin \bigg(-\dfrac{x}{3} \bigg) \in [-1;1]$ , тогда:

$\bigg((-1)^{k} \cdot \dfrac{\pi}{3} + \pi k \bigg) \in [-1;1],k \in \mathbb Z$ .

$k =0: (-1)^{0} \cdot \dfrac{\pi}{3} + \pi \cdot 0 = 1 \cdot \dfrac{\pi}{3} + 0 =\dfrac{\pi}{3} > 1$ , таким образом, так как $\forall k \in \mathbb Z : \bigg((-1)^{k} \cdot \dfrac{\pi}{3} + \pi k \bigg) \notin [-1;1] \Longrightarrow \boxed{ x \in \varnothing}$

б)

$(4x - 6) - 2 = \log_{\sqrt{5} }{(2x-5)}$

ОДЗ: $2x - 5 > 0 \Longleftrightarrow 2x > 5|:2 \Longleftrightarrow x > 2,5 \Longrightarrow \boxed{x \in (2,5;+\infty)}$

$4x - 6 - 2 = \log_{5^{0,5}}{(2x-5)}$

$4x - 8 =\dfrac{1}{0,5} \log_{5}{(2x-5)}$

$2(2x - 4) =2 \log_{5}{(2x-5)}|:2$

$2x - 4 =\log_{5}{(2x-5)}$

$2x - 4 -\log_{5}{(2x-5)} = 0$

Пусть $y = 2x - 4 -\log_{5}{(2x-5)};D(y) = (2,5;+\infty)$

$y' = ( 2x - 4 -\log_{5}{(2x-5)})' = (2x)' - (4)' - (\log_{5}{(2x-5)})' =$

$=2 - \dfrac{(2x- 5)'}{x \ln 5} = 2 - \dfrac{(2x- 5)'}{ \ln 5(2x- 5)} = 2 - \dfrac{2}{ \ln 5(2x- 5)}$

$y'' = (y')' = \bigg( 2 - \dfrac{2}{ \ln 5(2x- 5)}\bigg) ' = (2) ' - \bigg(\dfrac{2}{ \ln 5(2x- 5)}\bigg) ' = 0 - \dfrac{2}{\ln 5} \bigg( \dfrac{1}{2x-5} \bigg)' =$

$= - \dfrac{2}{\ln 5} \cdot \bigg( - \dfrac{2}{(2x-5)^{2} } \bigg) = \dfrac{4}{ \ln 5(2x- 5)^{2}}$

$y'' > 0$ при $\forall x \in D(y)$ , так как $\dfrac{4}{ \ln 5(2x- 5)^{2}} > 0$ при $x \in \mathbb R \backslash \{ 2,5 \}$ , а $2,5 \notin D(y)$ , следовательно функция выпукла вниз на всей своей области определения.

$y' =0$

$2 - \dfrac{2}{ \ln 5(2x- 5)} =0;$ ОДЗ: $x \neq 2,5$

$2 =\dfrac{2}{ \ln 5(2x- 5)}$

$2 \ln 5(2x- 5) = 2 |:2$

$\ln 5(2x- 5) =1$

$(2 \ln 5) \cdot x- 5 \ln 5 = 1$

$(2 \ln 5) \cdot x = 1 + 5 \ln 5 |:(2 \ln 5)$

$x = \dfrac{ 1 + 5 \ln 5}{2 \ln 5}$

Так как при $x = \dfrac{ 1 + 5 \ln 5}{2 \ln 5} \approx 2,8$ значение $y'' > 0$ и в данной точки производная первого порядка равна нулю, то точка $x = \dfrac{ 1 + 5 \ln 5}{2 \ln 5}$ является точкой локального минимума, но так как данная функция выпукла вверх на всей области определения, то данная точка есть точка глобального минимума.

$y \bigg( \dfrac{ 1 + 5 \ln 5}{2 \ln 5}\bigg) = 2 \bigg( \dfrac{ 1 + 5 \ln 5}{2 \ln 5}\bigg) - 4 -\log_{5}{\bigg(2 \bigg( \dfrac{ 1 + 5 \ln 5}{2 \ln 5}\bigg)-5\bigg)} \approx 1,92 > 0$

Тогда $\forall y \in E(y): y \geq y \bigg( \dfrac{ 1 + 5 \ln 5}{2 \ln 5}\bigg) > 0$ , тогда так $\nexists \ x \in D(y): y(x) = 0 \Longrightarrow \boxed{ x \in \varnothing}$