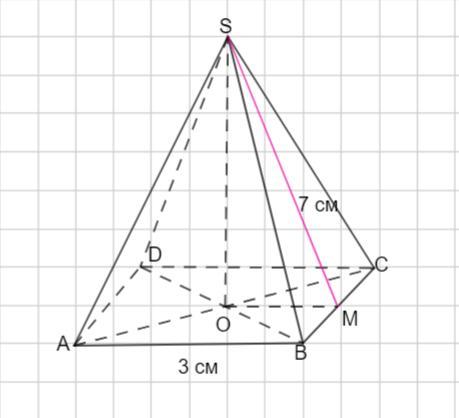
Предмет: Геометрия, автор: yadikarzkriya

Вычислить объем и поверхность правильной четырехугольной пирамиды, если сторона основания 3 см, а апофема 7 см.

Ответы

Автор ответа: lilyatomach

Ответ:

Площадь полной поверхности 51 см² , а объем пирамиды $\dfrac{3\sqrt{187} }{2}$ см³.

Объяснение:

Вычислить объем и поверхность правильной пирамиды, если сторона основания 3 см, а апофема 7 см.

Пусть дана SABCD - правильная пирамида. ABCD - квадрат со стороной 3 см. Апофема SМ = 7 см - это высота боковой грани.

Площадь полной поверхности пирамиды равна сумме площади основания и площади боковой поверхности .

Основание пирамиды квадрат. Площадь квадрата определяется по формуле: S= a² , a - сторона квадрата. Тогда площадь основания пирамиды будет : S= 3²= 3· 3 = 9 см².

Площадь боковой поверхности пирамиды равна полупроизведению периметра основания на апофему.

Найдем периметр квадрата по формуле Р =4·а ; Р =4 · 3 = 12 см.

Тогда площадь боковой поверхности пирамиды

$S =\dfrac{1}{2} \cdot 12 \cdot 7 = 6\cdot 7 = 42$ см².

Найдем площадь полной поверхности

S =42 + 9 = 51 cм².

Объем пирамиды определяется по формуле:

$V= \dfrac{1}{3} \cdot S \cdot H$

S - площадь основания , H - высота пирамиды.

Найдем высоту SО пирамиды из ΔSОМ - прямоугольного по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов .

SM² = SO² +OM²;

SO² = SM² - OM²;

OM = AB : 2 = 3: 2 = 3/2 cм.

$SO = \sqrt{7^{2} -\left(\dfrac{3}{2}\right) ^{2} } =\sqrt{49-\dfrac{9}{4} } =\sqrt{\dfrac{196-9}{4} } =\sqrt{\dfrac{187}{4} } =\dfrac{\sqrt{187} }{2}$