Висота рівнобедреного трикутника, опущена на бічну сторону, ділить її на відрізки завдовжки 4 см і 16 см, рахуючи від вершини кута при основі. Знайдіть основі рівнобедреного трикутника

Відповідь:

Дано:

Висота рівнобедреного трикутника, опущена на бічну сторону, ділить її на відрізки завдовжки  4 см і 16 см, рахуючи від вершини кута при основі

Знайти основу рівнобедреного трикутника.

Разв"язання:

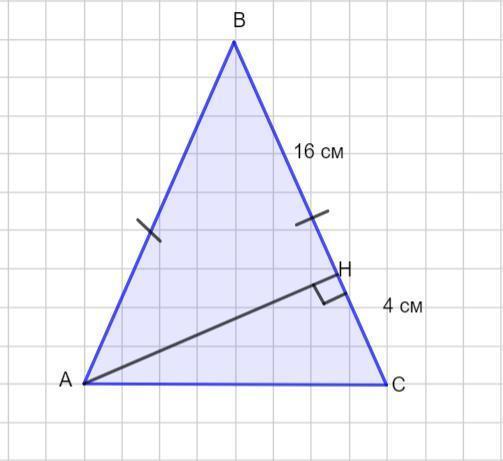
Нехай дано Δ АВС – рівнобедрений, АВ = ВС.

Висота АН.

Точка Н ділить бічну сторону на відрізки СН = 4 см та ВН = 16 см. Тоді сторона ВС = ВН + НС = 16 + 4 = 20 см.

Оскільки АВ = ВС, то АВ = 20 см

Розглянемо ΔАНВ – прямокутний.                                                                 Знайдемо АН за теоремою Піфагора: у прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

АВ²= АН²+ВН²

АН²=АВ²-ВН²

АН=√АВ²-ВН²

АН=√ 20² -16² =  √ (20-16)*(20+16)=√4*36=2*6=12см  

Розглянемо ΔАНС - прямокутний і знайдемо основу АС рівнобедреного трикутника за теоремою Піфагора

АС²=АН²+НС²

АС=√АН²+НС²

АС=√ 12² -4² =  √ 144+16=√160=√16*10=4√10см  

Відповідь: основа рівнобедреного трикутника дорівнює 4√10 см.

Пояснення: