Предмет: Математика, автор: yanerovip92

Найти скорость движения точки в конце четвертой секунды.

Приложения:

ГАЗ52: Скорость - это производная от пути. V=14x+5/(5x-15)-e^(x-4)
V(4)=14•4+5/(5•4-15)-e^(4-4)=
=56+1-1=56

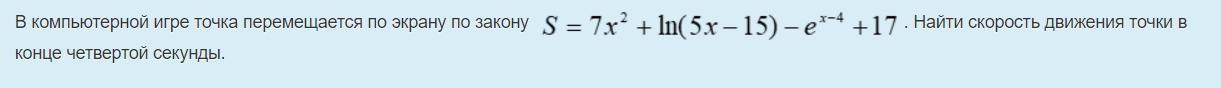
Ответы

Автор ответа: polarkat

Скорость - это производная от пути, то есть

$\dot{v}=\left(\ln\left(5\,x-15\right)\right)'-\left({e}^{x-4}\right)'+7\cdot \left({x}^{2}\right)'+\left(17\right)'=$

$=\dfrac{1}{5\,x-15}\cdot \left(5\,x-15\right)'-{e}^{x-4}\cdot \left(x-4\right)'+7\cdot 2\cdot x+0=-{e}^{x-4}+\dfrac{5}{5\,x-15}+14\,x$

$\dot{v}(4)=-1+1+56=56$

Производную обычно обозначают штрихом $f'(x)$ , но так как задача по физике, хоть и математическая, то обозначается через точку, всё же эти физика. Обозначения разные, а смысл один!