Предмет: Алгебра, автор: Xonda7777

Исследовать сходимости рядов.

Приложения:

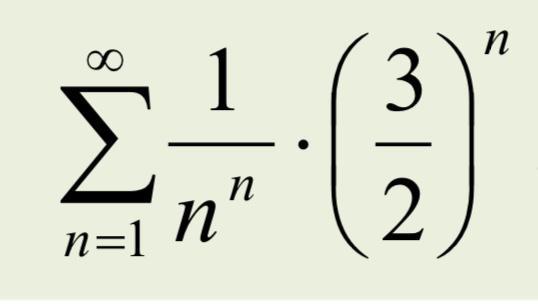
antonovm: сходится , радикальный признак Коши примените

Xonda7777: Пожалуйста можете скинуть решение сделанное вами?

antonovm: корень степени n из a(n) равен 1/n *3/2 , предел этой последовательности равен 0 < 1 и значит ряд сходится по признаку Коши ( это решение )

Xonda7777: Спасибо

Ответы

Автор ответа: Alnadya

Решение.

$\bf \sum \limits _{n=1}^{\infty }\dfrac{1}{n^{n}}\cdot \Big(\dfrac{3}{2}\Big)^{n}$

Применим достаточный радикальный признак сходимости Коши .

$\bf \lim \limits _{n \to \infty}\sqrt[n]{a_{n}} =\lim \limits _{n \to \infty}\sqrt[n]{\dfrac{1}{n^{n}}\cdot \Big(\dfrac{3}{2}\Big)^{n}}=\lim \limits _{n \to \infty}\Big(\dfrac{1}{n}\cdot \dfrac{3}{2}\Big)=\Big[\ \dfrac{3}{\infty }\ \Big]=0 < 1$

Так как получили в пределе константу, меньшую 1 , то ряд сходится .

Приложения:

Xonda7777: Спасибо

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Українська мова, автор: JolydiPopsa

скласти речення З фразеологізмом "В одну дудку грати"

1 год назад

Предмет: Право, автор: Аноним

Уявіть себе народними депутатами України або депутатами місцевої Ради. На обговорення вашої Ради винесено питання про попередження та зниження рівня злочинності. .Визначте причини правопорушень та !запропонуйте заходи щодо профілактики та зниження рівня злочинності!

1 год назад

Предмет: Математика, автор: tsakuri0

вычислите
tg 1290
sin 1470

1 год назад

Предмет: Биология, автор: tereschkab

объясни значение крови для поддержания постоянства внутренней среды организма

7 лет назад

Предмет: Русский язык, автор: tonakanyanqnqush

2. ЗАПИШИТЕ ПРЕДЛОЖЕНИЯ, ВЫБРАВ ИЗ СКОБОК НУЖНУЮ ФОРМУ ЛИЧНОГО МЕСТОИМЕНИЯ. 1. Мы попросили (её, неё) остаться. 2. Навстречу (ему, нему) шёл какой-то старик. 3. Навстречу (ей, ней) выбежала собака. 4. Это Ани. Мы дружим с (ей, ней) со школы. 5. Это Армен. Я познакомился с (им, ним) в университете.

7 лет назад