Предмет: Математика, автор: toltol1238

Правильный ответ первый, но не могу понять откуда берется -2 в ответе.
Приложение в телефоне показывает такой ход решения 3x+6≤0 из которого получается x≤-2. Разве аргумент логарифма может быть отрицательным?

Приложения:

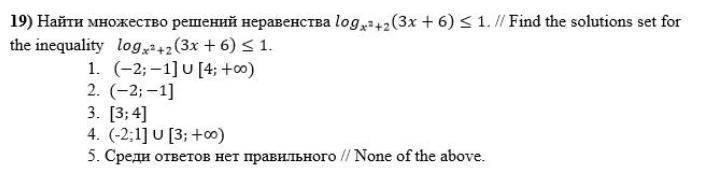
Ответы

Автор ответа: 7x8

1

Ответ:

$x\in(-2;-1]\cup[4;+\infty)$

Пошаговое объяснение:

$log_{x^2+2}(3x+6) \le 1$

ОДЗ:

1)

$x^2+2>0$

$x\in R$

2)

$x^2+2 \neq 1$

$x\in R$

3)

$3x+6>0$

$3x>-6\ \ \ |:3$

$x>-2$

$x\in(-2;+\infty)$

$log_{x^2+2}(3x+6) \le 1$

Область значений функции $x^2+2$

$[2;+\infty)$

так что

$log_{x^2+2}(3x+6) \le log_{x^2+2}(x^2+2)$

$3x+6 \le x^2+2$

$3x+6-x^2-2 \le 0$

$-x^2+3x-4 \le 0\ \ \ |:(-1)$

$x^2-3x-4 \ge 0$

$D=(-3)^2-4\cdot1\cdot(-4)=9+16=25$

$\sqrt{D}=\sqrt{25}=5$

$x_1=\frac{3-5}{2\cdot1}=\frac{-2}{2}=-1$

$x_2=\frac{3+5}{2\cdot1}=\frac{8}{2}=4$

$x\in(-\infty;-1]\cup[4;+\infty)$

$x\in(-2;-1]\cup[4;+\infty)$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: Lopa1223o9e832

Помогите,,,,,,,вджв вьдвщдц в. А авв

1 год назад

Предмет: Українська мова, автор: polina4783

12.Складіть речення з фразеологізмами як водою змило, як торішні бублики
СРОЧНО,ДАМ 10 БАЛІВ!!!

1 год назад

Предмет: Русский язык, автор: getz4747

5. Прочитай. Найди одинаковые слова с разными ударениями. Назови их. На юге Казахстанавращивают хлопок. Дети услышали громкий хлопок. слова. Напишите в тетради

1 год назад

Предмет: Геометрия, автор: YouMyGalaxy

с решением пожалуйста

7 лет назад

Предмет: Геометрия, автор: YouMyGalaxy

Геометрия
____________

7 лет назад