Предмет: Геометрия, автор: grekdara94

Помогите плизззз!!!!!!

Приложения:

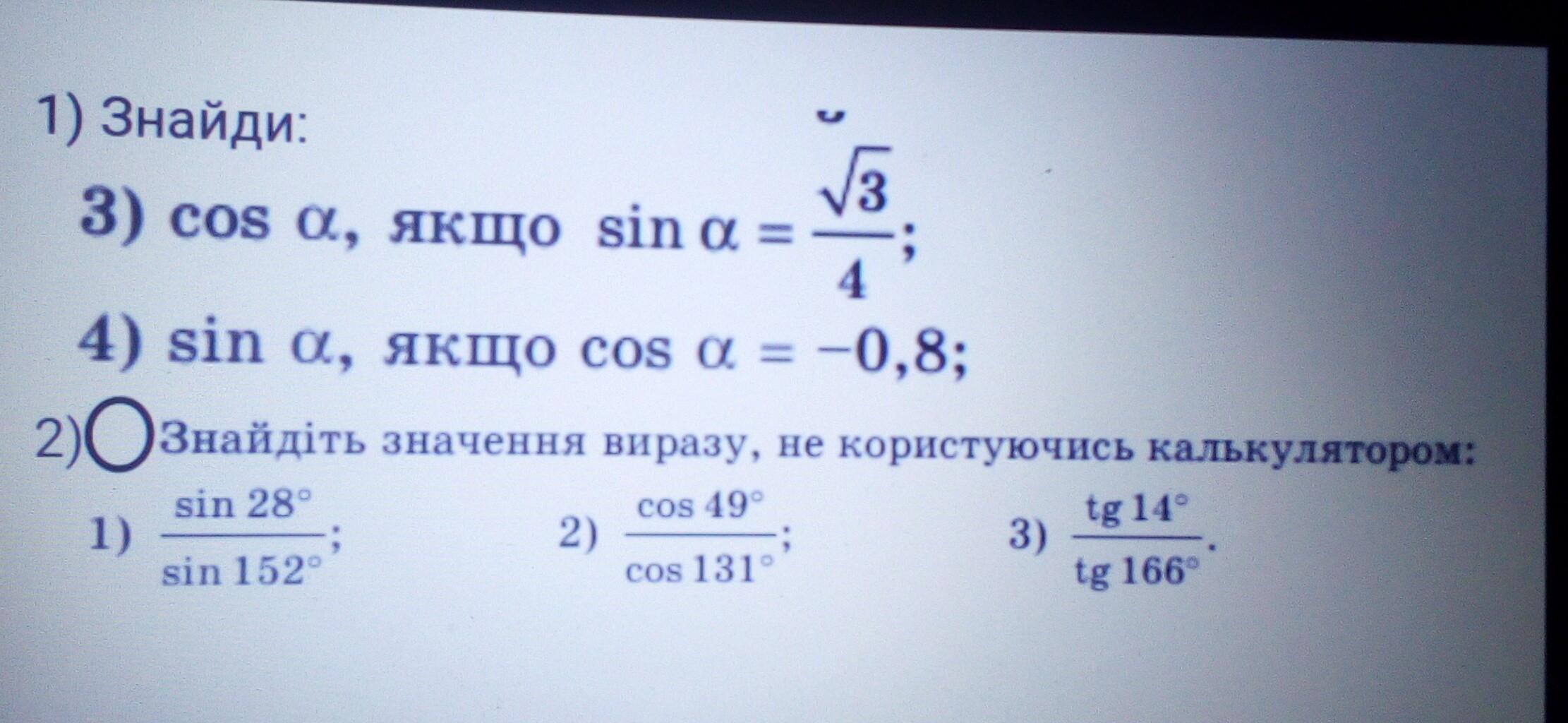
Ответы

Автор ответа: axatar

Ответ и Объяснение:

1) Информация. Основное тригонометрическое тождество:

sin²α + cos²α = 1.

3) Требуется найти cosα, если $\sin\alpha =\dfrac{\sqrt{3} }{4}$ .

Подставим известное значение в основное тригонометрическое тождество:

$\tt \bigg (\dfrac{\sqrt{3} }{4} \bigg )^2+cos^2\alpha =1 \\\\\dfrac{3}{16} +cos^2\alpha =1 \\\\cos^2\alpha =1-\dfrac{3}{16}\\\\cos^2\alpha =\dfrac{13}{16}\\\\cos\alpha = \pm \sqrt{\dfrac{13}{16}} \\\\cos\alpha = \pm \dfrac{\sqrt{13} }{4} .$

4) Требуется найти sinα, если $\cos\alpha =-0,8$ .

Подставим известное значение в основное тригонометрическое тождество:

sin²α + (-0,8)² = 1

sin²α + 0,64 = 1

sin²α = 1 - 0,64

sin²α = 0,36

sinα = ±0,6.

2) Требуется найти значение выражения не используя калькулятор.

Формулы приведения:

a) sin(180°-α) = sinα;

b) cos(180°-α) = -cosα;

c) tg(180°-α) = -tgα.

$1) \; \tt \displaystyle \frac{sin28^0}{sin152^0}= \frac{sin(180^0-152^0)}{sin152^0}= \frac{sin152^0}{sin152^0}= 1;$

$2) \; \tt \displaystyle \frac{cos49^0}{cos131^0}= \frac{cos(180^0-131^0)}{cos131^0}= \frac{-cos131^0}{cos131^0}= -1;$

$3) \; \tt \displaystyle \frac{tg14^0}{tg166^0}= \frac{tg(180^0-166^0)}{tg166^0}= \frac{-tg166^0}{tg166^0}= -1.$

#SPJ1

grekdara94: помогите пожалуйста ещё с одним задание в профиле ‼️

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Право, автор: bira8743

есе за темою:
які проблеми з дотримання прав людини існують в сучасному світі

1 год назад

Предмет: Українська мова, автор: Huger892

ПОМОГИТЕ ПОЖАЛУЙСТА С УПРАЖНЕНИЕМ

1 год назад

Предмет: Алгебра, автор: kristinalutsenko76

Яке число треба відняти від численика та знаменника дробу 5/8 щоб отримати 2/3.

Помогите плизззз!!!!!!​

Ответы

Помогите плизззз!!!!!!