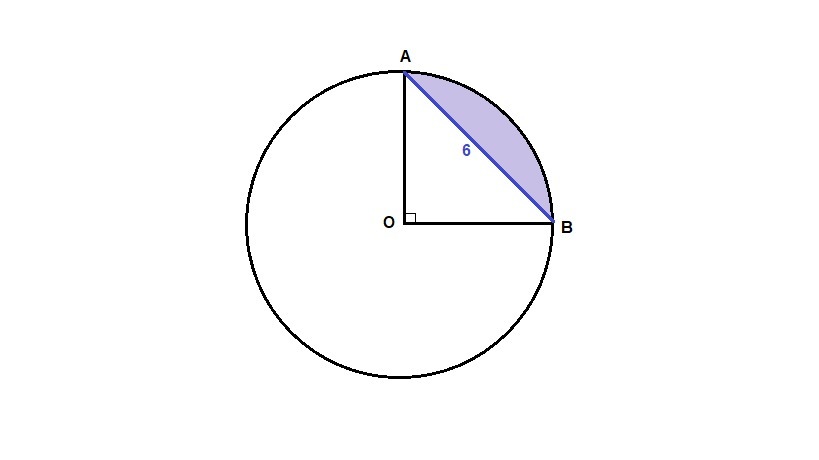
Дано: АВ=6см, угол АОВ=90. Найти: а) длину дуги АВ; б) площадь сектора АОВ; в) площадь меньшей части круга, на которые его делит хорда АВ

а) ОА = ОВ как радиусы,

По теореме Пифагора:

R² + R² = AB²

2R² = 36

R² = 18

R = √18 = 3√2 см

Длина дуги АВ:

l = 2πR · α / 360°

l = 2π · 3√2 · 90° / 360° = 1,5√2π см

б) Sсект = πR² · α / 360°

Sсект = π · (3√2)² · 90° / 360° = 4,5π см²

в) Чтобы найти площадь закрашенного сегмента, надо от площади сектора отнять площадь треугольника АОВ:

Sсегм = Sсект - Saob

Saob = 1/2 AO · OB = 1/2 R² = 1/2 · (3√2)² = 1/2 · 18 = 9 см²

Sсегм = 4,5π - 9 = 9(π/2 - 1) см²