Предмет: Геометрия,
автор: SamPay
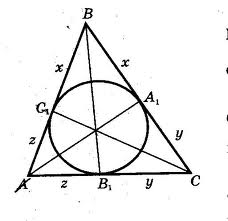
в треугольник aBC вписана окружность, которая касается стороны AB в точке C1, стороны BC в точке A1, стороны CA в точке b1. Найдите периметр треугольника если Ас1=3, ba1=5, cb1=2
Ответы
Автор ответа:
0
1) Учитывая, что отрезки касательных из внешней точки к окружности равны, получим рисунок, из которого видно АВ1=АС1=3, ВА1=ВС1=5, СВ1=СА1=2.
2) Р= АВ1+АС1+ ВА1+ВС1+ СВ1+СА1=6+10+4= 20.
Ответ: 20.
Приложения:
Автор ответа:
0
Вписанная окружность делит каждую сторону на отрезки, и по свойству касательных, проведенных из одной точки к окружности, эти отрезки равны, если имеют общую вершину треугольника в качестве конца :)).
АС1 = АВ1 = 3, ВА1 = ВС1 = 5, СА1 = СВ1 = 2.
Поэтому сумма всех сторон равна удвоенной сумме трех различных таких отрезков,
Р = 2*(3 + 5 + 2) = 20
Приложения:

Интересные вопросы
Предмет: История,
автор: nmuraveva2009
Предмет: Обществознание,
автор: romarinoooa
Предмет: Литература,
автор: buchwheat656
Предмет: Математика,
автор: Владик2002
Предмет: Математика,
автор: Human