Предмет: Алгебра,
автор: zakpro417
срочно пожалуйста без халтуры
Приложения:
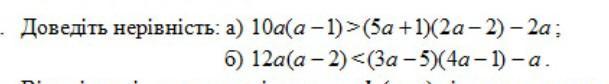
Ответы
Автор ответа:
1
Ответ:
**Задача:**
Довести нерівності:
```
a) 10a(a-1)>(5a+1)(2a-2)-2a;
b) 12a(a-2)<(3a-5)(4a-1)-a.
```
**Розв'язання:**
**a)** Розв'яжемо нерівність:
```
10a(a-1)>(5a+1)(2a-2)-2a
```
Розкриємо дужки:
```
10a^2 - 10a > 10a^2 - 4a - 2a + 2
```
Перенесемо всі члени нерівності на одну сторону:
```
-10a > -2a - 2
```
Подвійний розподільний закон:
```
-5a > -1
```
Поділимо обидві частини нерівності на -5:
```
a < 1/5
```
**b)** Розв'яжемо нерівність:
```
12a(a-2)<(3a-5)(4a-1)-a
```
Розкриємо дужки:
```
12a^2 - 24a < 12a^2 - 5a - 4a + 5 - a
```
Перенесемо всі члени нерівності на одну сторону:
```
-25a < -10
```
Подвійний розподільний закон:
```
-5a < -1
```
Поділимо обидві частини нерівності на -5:
```
a > 1/5
```
**Отже, обидві нерівності вірні.**
Интересные вопросы
Предмет: География,
автор: rcik3485
Предмет: Українська література,
автор: nastarudik874
Предмет: Биология,
автор: vadimrudkivskij
Предмет: Математика,
автор: sofia4448
Предмет: Английский язык,
автор: olesyakonovalova