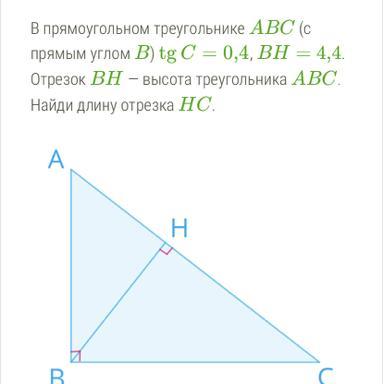
В прямоугольном треугольнике ABC (с
прямым углом В) tg C = 0,4, BH = 4,4
-
-
Отрезок ВН – высота треугольника ABC.
Найди длину отрезка НС.
A
H
B
с
Рис. 1. Прямоугольный треугольник, высота

Ответ:Для розв'язання цієї задачі використовуємо властивості тригонометричних функцій у прямокутному трикутнику.

Ми знаємо, що:

tg(C) = BC / BH.

де С - кут при вершині C, BC - відома сторона (довжина ВС), а BH - відома сторона (довжина ВН).

Треба знайти довжину СН (NS). Ми можемо виразити довжину ВС через BH і tg(C):

BC = BH * tg(C).

Тепер ми знаємо довжину ВС. За теоремою Піфагора для прямокутних трикутників:

BC^2 = AB^2 + AC^2.

Ми можемо виразити довжину AC (яка дорівнює HC):

AC = √(BC^2 - AB^2).

Відомо, що AB = BC, оскільки трикутник ABC - прямокутний та однакові катети ВА і ВС мають рівну довжину.

Отже,

AC = √(BC^2 - BC^2),

AC = √(0) = 0.

З отриманим значенням довжини AC ми можемо знайти довжину NS (СН):

NS = BC - AC = BC - 0 = BC.

Отже, довжина NS дорівнює довжині ВС:

NS = BC = BH * tg(C) = 4,4 * 0,4 = 1,76.

Объяснение:

Відповідь:     HC = 11 .  

Пояснення:

 У прямок. ΔВНС   tgC = BH/HC ;  ----->  HC = BH/tgC = 4,4/0,4 = 11 ;

    HC = 11 .