Предмет: Геометрия, автор: sonyalunkina12

Докажите что четырехугольник ABCD является прямоугольником если A(2;2)B(3;-1)C(-3;-3)D(-4;0)

Ответы

Автор ответа: axatar

Ответ и Объяснение:

Информация. 1) Если в четырехугольнике противолежащие стороны попарно равны, то этот четырехугольник – параллелограмм.

2) Если у параллелограмма есть прямой угол или равны диагонали, то он является прямоугольником.

3) Расстояние между точками M(x₁; y₁) и N(x₂; y₂) вычисляется по формуле

$\tt d(MN)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} .$

Дано:

Четырехугольник ABCD

A(2; 2), B(3; -1), C(-3; -3), D(-4;0).

Докажем, что этот четырехугольник - прямоугольник.

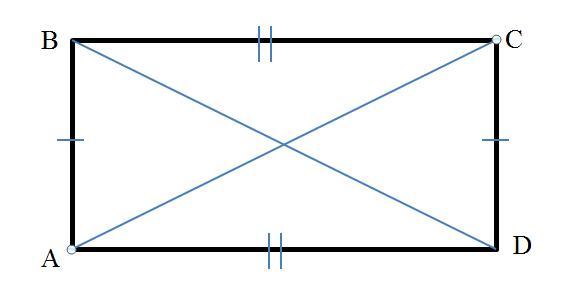
Для этого, учитывая вышеприведённые свойства достаточно показать, что для сторон AB=CD и BC=AD, для диагоналей: AC=BD.

Вычислим длины:

$\tt d(AB)=\sqrt{(2-3)^2+(2-(-1))^2} =\sqrt{1+9} =\sqrt{10}; \\\\d(CD)=\sqrt{(-3-(-4))^2+(-3-0)^2} =\sqrt{1+9} =\sqrt{10}; \\\\d(AB)=d(CD);\\\\d(BC)=\sqrt{(3-(-3))^2+(-1-(-3))^2} =\sqrt{36+4} =\sqrt{40}; \\\\d(AD)=\sqrt{(2-(-4))^2+(2-0)^2} =\sqrt{36+4} =\sqrt{40};\\\\d(BC)=d(AD);$