Предмет: Алгебра, автор: vikatorgac330

помогите пожалуйста ​

Приложения:

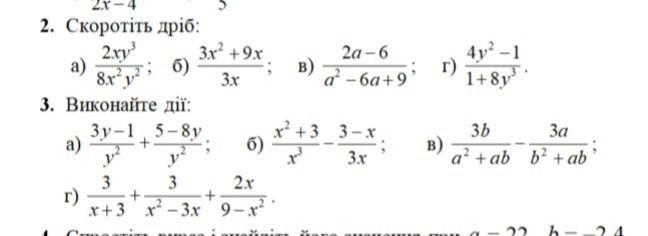
Ответы

Автор ответа: vodoleyka2501
1

Ответ:

Объяснение:

2.

a) = \frac{y}{4x}

б) = \frac{3x(x+3)}{3x} = x+3

в) = \frac{2(a-3)}{(a-3)^{2} } = \frac{2}{a-3}

г) = \frac{(2y-1)(2y+1)}{(1+2y)(1-y+y^{2})\\} = \frac{2y-1}{1-y+y^{2} }

3.

a) = \frac{3y-1+5-8y}{y^{2} } = \frac{4-5y}{y^{2} }

б) = \frac{3(x^{2} +3)-x^{2} (3-x)}{3x^{3} } = \frac{3x^{2} +9-3x^{2} +x^{3} }{3x^{3} } = \frac{3}{x^{3} } +\frac{1}{3}

в) = \frac{3b}{a(a+b)} - \frac{3a}{b(b+a)} = \frac{3b^{2}-3a^{2} }{ab(a+b)} = \frac{3(a+b)(a-b)}{ab(a+b)} = \frac{3a-3b}{ab} = \frac{3}{b} - \frac{3}{a}

г) = \frac{3}{x+3} + \frac{3}{x(x-3)} +\frac{2x}{(3-x)(3+x)} = \frac{3x(x-3)+3(x+3)-2x^{2} }{x(x-3)(x+3)} = \frac{3x^{2} -9x+ 3x+9-2x^{2} }{x(x-3)(x+3)}= \frac{x^{2}-6x+9 }{x(x-3)(x+3)} = \frac{(x-3)^{2} }{x(x-3)(x+3)} = \frac{x-3}{x^{2} +3x}

vikatorgac330: спасибо
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык, автор: muhammadaziz2802010
Образуйте от данных чисел порядоковые числительные и запишите их.80,87,371,14,77
1 год назад
Предмет: Химия, автор: Dashapchela338
скільки потрібно зважити H2SO3 щоб було рівно 2 моль?
1 год назад
Предмет: Биология, автор: Stasiiloveskz
"Укажи ознаку яка є спiльною для Окуня рiчкового та дельфiна чорноморського"
А.шкiра,у якiй немає залоз.
Б.органи дихання-зябра.
В.покриви тiла-луска.
Г.обтiчна форма тiла.​
1 год назад
Предмет: Русский язык, автор: matvienkoaleksandr81
30. Прочитайте существительные, обратите внимание на бук-
вы и, е в суффиксах -ик, -ек. В каком суффиксе гласный выпадает,
ав каком — не выпадает?
Сделайте вывод. Если гласный в суффиксе существительно-
го выпал, то пишите суффикс если он не выпал, то пишите
суффикс
Носик носика, носику, носиком.
Звоночек звоночка, звоночку, звоночком, о звоночке.​
7 лет назад
Предмет: Русский язык, автор: balalaevavika763
Все баллы свои отдаю,Сочинение на тему "почему я выбрала профессию гостиничное дело" нужно просто оооооочень срочно,помогитеееее
7 лет назад