Предмет: Алгебра, автор: fctdgsygfdhngfxzgsac

Знайти границі послідовності.

Приложения:

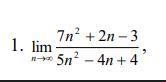
Ответы

Автор ответа: 7x8

1

Ответ:

$\displaystyle 1\frac{2}{5}$

Объяснение:

$\displaystyle \lim_{n\to \infty}\frac{7n^2+2n-3}{5n^2-4n+4}=\lim_{n\to \infty}\frac{\frac{7n^2}{n^2}+\frac{2n}{n^2}-\frac{3}{n^2}}{\frac{5n^2}{n^2}-\frac{4n}{n^2}+\frac{4}{n^2}}=\\\\\lim_{n\to \infty}\frac{7+\frac{2}{n}-\frac{3}{n^2}}{5-\frac{4}{n2}+\frac{4}{n^2}}=\frac{7}{5}=1\frac{2}{5}$

fctdgsygfdhngfxzgsac: спасибо большое))

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: blogerjac

СРОЧНО ДАМ 20БАЛЛОВ ПОЖАЛУЙСТА ПОМОГИТЕЕЕЕЕЕЕЕ

1 год назад

Предмет: Алгебра, автор: derevodub30000

в уравнении x2+px+3=0 один из корней равен -1. найти второй корень и коэффициент p

1 год назад

Предмет: Математика, автор: a8975174

Площадь фигуры срочнооо

1 год назад

Предмет: Математика, автор: abo2301

За день в кондитерской изготовили 12 тортов. Это на 24 штуки
меньше, чем пирожных. Во сколько раз меньше изготовили
тортов, чем пирожных?

7 лет назад

Предмет: Математика, автор: yukhimets87

Різницю чисел 18 і 19 збільшити у 8 разів

7 лет назад