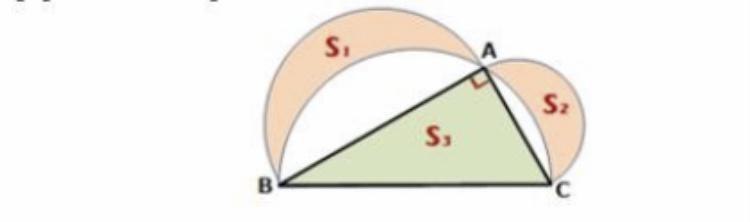
На гіпотенузі ВС = с та катетах AB = а та АС = 3 прямокутного трикутника АВС, як на діаметрах, побудовані півкола. Доведіть, що площа цього трикутника дорівнює сумі площ зафароованих «серпиків»
ПОМОГИТЕ ПОЖАЛУЙСТА

Для доведення цього твердження нам слід використовувати геометричні властивості фігур та використовувати площі півкіл. Давайте подивимося на кожен крок окремо:

1. Почнемо з трикутника ABC. Його площу позначимо як S.

2. Побудуємо півкола на катетах AB та AC як діаметрах. Площу кожного з цих півкіл позначимо як S1 і S2.

3. Знаючи радіуси цих півкіл, ми можемо обчислити S1 і S2 за допомогою формули для площі круга: S = (π * r^2) / 2, де r - радіус півкола.

4. Сума площ півкілів S1 і S2 дорівнює сумі площ зафарбованих "серпиків", які утворюються внаслідок півкіл.

5. Таким чином, площа трикутника ABC дорівнює сумі площ зафарбованих "серпиків", тобто S = S1 + S2.

Отже, ми довели, що площа трикутника ABC дорівнює сумі площ зафарбованих "серпиків".