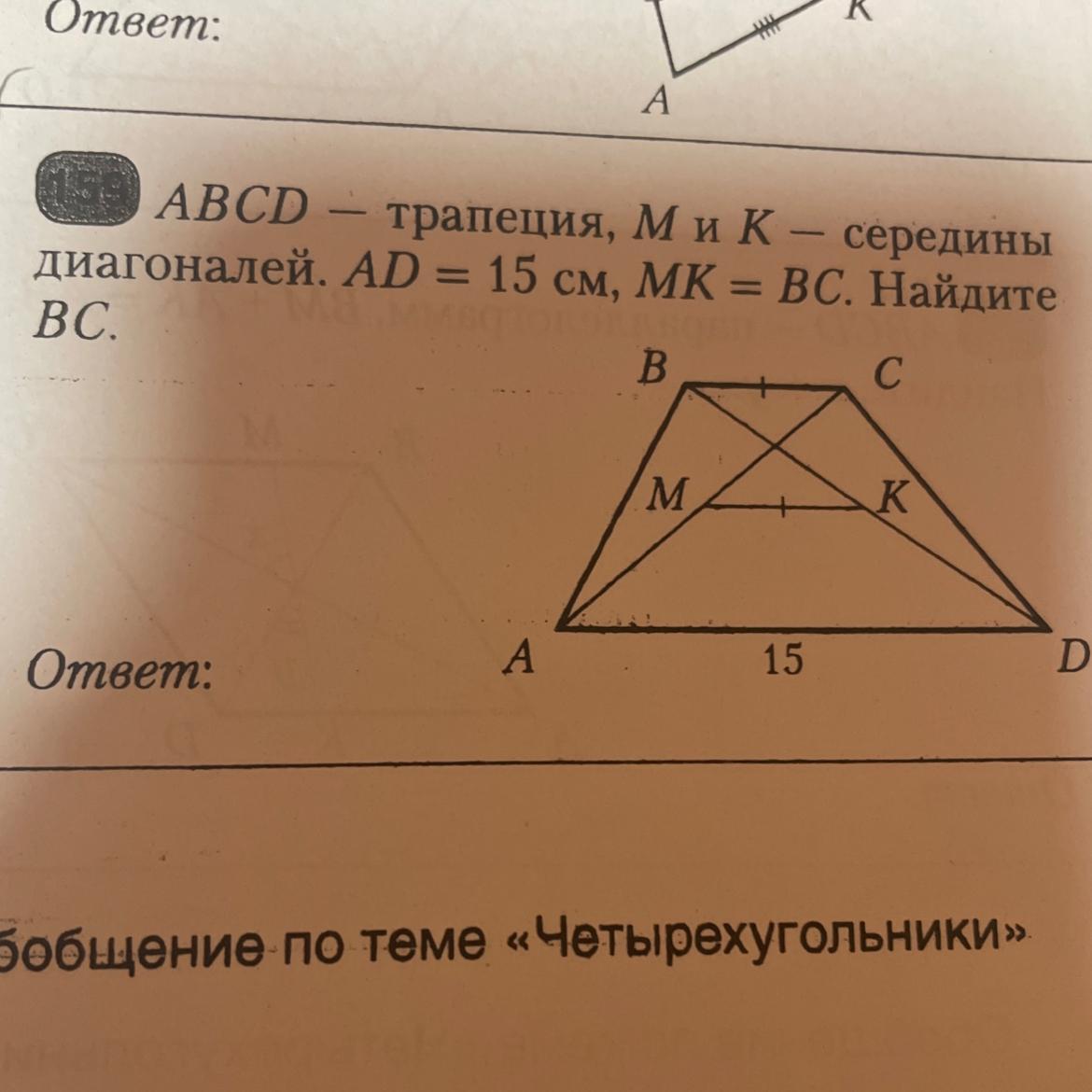
ABCD- трапеция, M и K - середины диагоналей. AD = 15 см, MK = BC. Найдите BC.

Ответ:

Для решения задачи воспользуемся свойствами серединных перпендикуляров в трапеции.

По свойству серединных перпендикуляров в трапеции, диагонали трапеции делятся друг на друга пополам. То есть, MK = BC.

Также известно, что MK = BC, поэтому можно записать:

MK = BC

Также известно, что MK - середина диагонали AC, поэтому можно записать:

MK = 1/2 * AC

Из условия задачи известна длина стороны AD, поэтому можно записать:

AC = AD + CD

AC = 15 + CD

Теперь подставим значения AC и MK в уравнение:

1/2 * (15 + CD) = BC

Упростим уравнение:

15 + CD = 2 * BC

CD = 2 * BC - 15

Итак, длина отрезка BC равна 2 * BC - 15 см.

Объяснение: