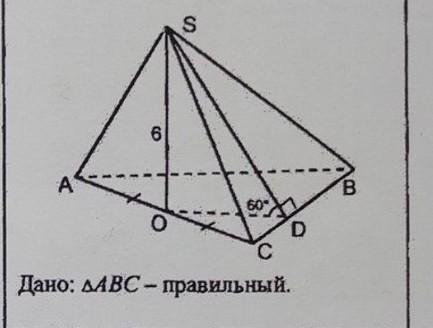
помогите пожалуйста найти площадь пирамиды.​

Ответ:

Площадь полной поверхности пирамиды равна 24+48√3 ед.кв.

Объяснение:

∆SOD- прямоугольный треугольник. С углами ∠SOD=90°; ∠SDO=60°; ∠OSD=30°.

По свойству этого треугольника катет против угла 30° в два раза меньше гипотенузы.

OD=x катет против угла 30°

SD=2x гипотенуза.

Теорема Пифагора:

SD²-OD²=SO²

(2x)²-x²=6²

3x²=36

x²=12

x=2√3 ед. OD

SD=2x=2*2√3=4√3 ед.

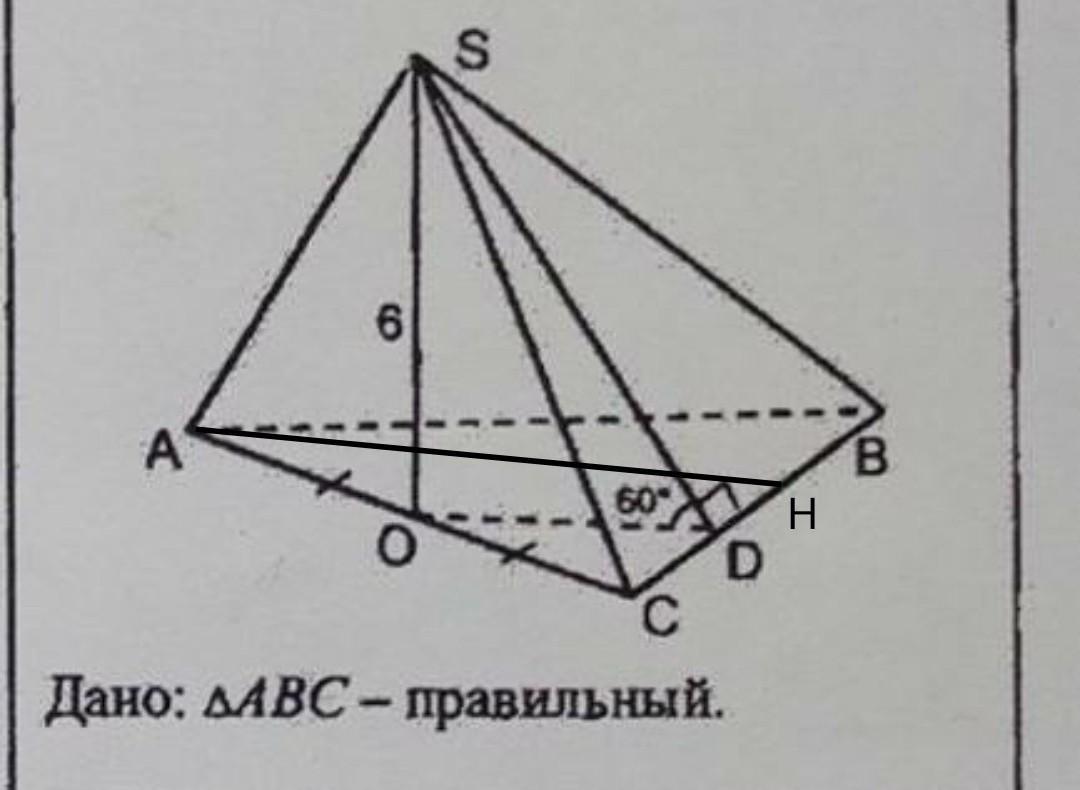
АН=2*ОD=2*2√3=4√3ед высота треугольника ∆АВС;

АН=АВ√3/2; →

АВ=2*АН/√3=2*4√3/√3=8eд.

S(∆ABC)=½*BC*AH=½*8*4√3=

=16√3ед.кв.

S(∆ASC)=½*SO*AC=

=½*6*8 =24 ед.кв.

S(∆SCB)=½*SD*CB=½*4√3*8=

=16√3ед.кв.

∆SCB=∆SAB;

Sб=S(∆ASC)+2*S(∆SCB)=24+2*16√3=

=24+32√3 ед.кв.

Sп=S(∆ABC)+Sб=16√3+24+32√3=

=24+48√3 ед.кв.