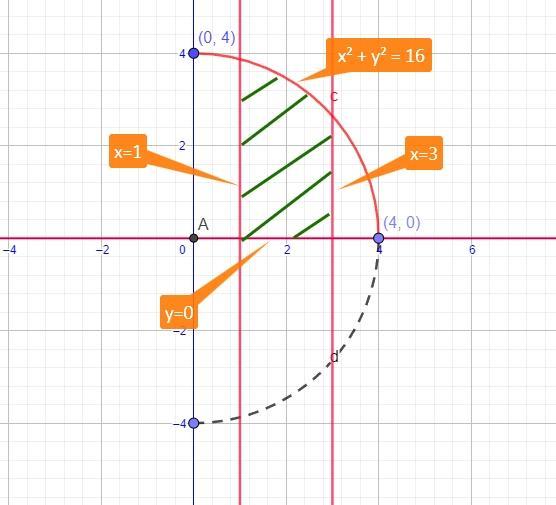
обчислити об'єм тіла утвореного обертанням навколо осі х фігури, обмеженої дугою кола х² + y² = 16, яка лежить у першій чверті, та прямими x = 1, x = 3, y = 0

Ответ:

Пошаговое объяснение:

Формула  объема тела, образованного вращением вокруг оси х кривой y(x)

Делаем чертеж. Определяемся с границами интегрирования

а = 1;  b=3;

Находим y²(x)

х² + y² = 16   ⇒   y² = 16- х²

И теперь считаем интеграл