Предмет: Математика, автор: godmercury39

Знайти інтеграл з розписаними кроками

Приложения:

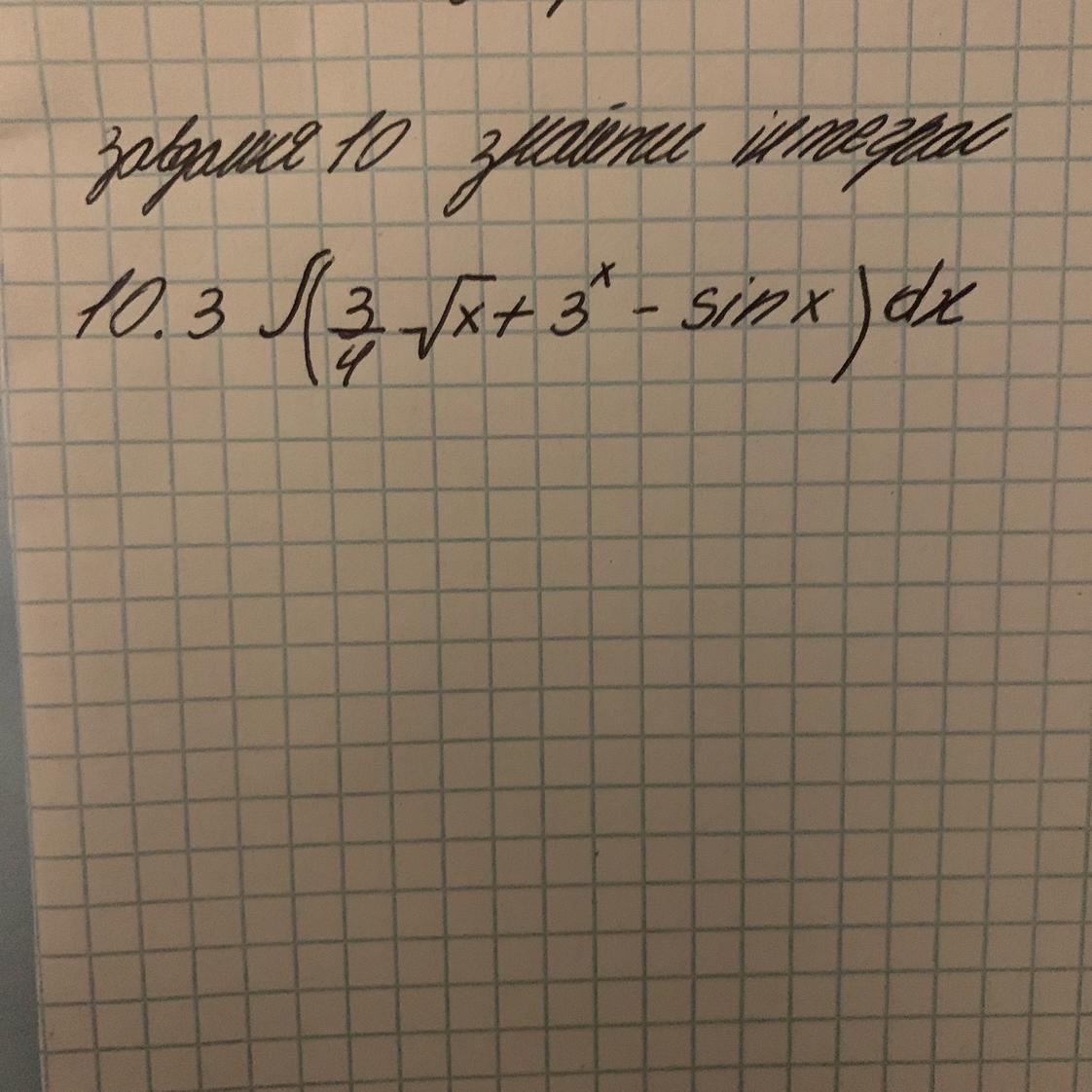
Ответы

Автор ответа: pushpull

1

Ответ:

$\displaystyle \frac{\sqrt{x^3} }{2} +\frac{3^x}{ln(3)} +cos(x)+C$

Пошаговое объяснение:

$\displaystyle \int \bigg(\frac{3}{4} \sqrt{x} +3^x-sin(x)\bigg)dx= \frac{3}{4} \int \bigg(\sqrt{x}\bigg)dx +\int 3^x\; dx-\int \bigg(sin(x)\bigg)dx=\\\\\\=\frac{3}{4}*\frac{2}{3} \sqrt{x^3} +\frac{3^x}{ln(3)} +cos(x)+C=\frac{\sqrt{x^3} }{2} +\frac{3^x}{ln(3)} +cos(x)+C$

godmercury39: Можеш ще папу завдань на інтеграли вирішити ?

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: afoninlife

пожалуйста напишите мини-сочинение на одну из тем.
пожалуйста это срочно !!!!

1 год назад

Предмет: Математика, автор: Lelovek

774. Выполните 2 2 .6 15 4 1) 3 2) 30 л -1 действия: 1 .1 3 8 1 5 12 7 12 +4 5 9; 19 9. 3)- 36 17 35 1 11 34

1 год назад

Предмет: Алгебра, автор: Rozzzbijnyk

Срочно у меня скоро сдача с обьяснением пошогово!!!

1 год назад

Предмет: Биология, автор: matrixer

Укажи, какие признаки характерны для человека и млекопитающих животных (Вставь соответствующие буквы в алфавитном порядке, без пробелов): . З — альвеолярное лёгкое. Б — наличие вороньих костей. Д — правая дуга аорты. О — выкармливание детёнышей молоком. М — трёхкамерное сердце. Т — левая дуга аорты.

7 лет назад

Предмет: Другие предметы, автор: c29mk6qzzs

Инфо час 7 класс ,,По страницам детских газет и журналов’’ Помогите!

7 лет назад