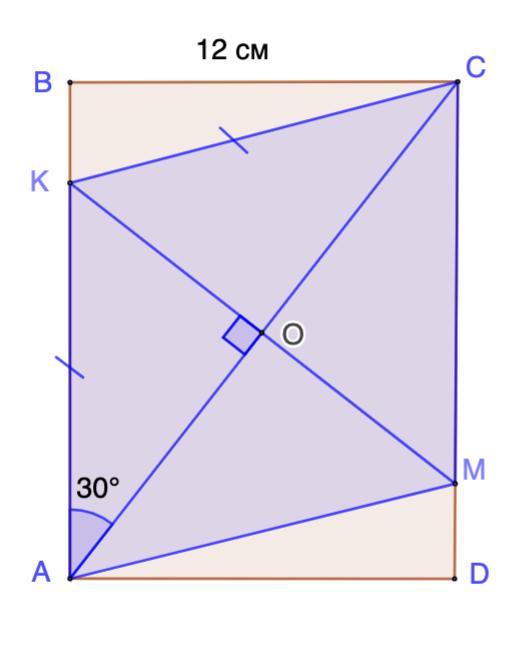
На сторонах AB и CD прямоугольника ABCD взяты точки K и M так, что AKCM - ромб. Диагональ AC составляет со стороной AB угол 30 градусов. Найдите сторону ромба, если меньшая сторона прямоугольника ABCD равна 12.

Ответ:

Сторона ромба равна 8√3.

Объяснение:

На сторонах AB и CD прямоугольника ABCD взяты точки K и M так, что AKCM - ромб. Диагональ AC составляет со стороной AB угол 30 градусов. Найдите сторону ромба, если меньшая сторона прямоугольника ABCD равна 12.

Дано: ABCD - прямоугольник;

К ∈ АВ; М ∈ CD;

AKCM - ромб;

BC = 12;   ∠ВАС = 30°.

Найти: АК

Решение:

Рассмотрим ΔАВС - прямоугольный;

ВС = 12;   ∠ВАС = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒   АС = 2 ВС = 24.

Рассмотрим ΔАКО.

• Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.

⇒   КМ ⊥ АС,   АО = ОС = 12.

∠ ВАС = 30°   ⇒   АК = 2 ОК

Пусть ОК = х, тогда АК = 2х

По теореме Пифагора:

АК² = ОК² + АО²

4х² = х² + 144

3х² = 144

х = √48

х = 4√3

ОК = 4√3, тогда сторона ромба АК = 2х = 8√3