Предмет: Алгебра, автор: gulbahoraktamova40

Докажите, что если а > 0, то: a + 4/2 + a + 9/2 > 5√а
даю 15 баллов

Приложения:

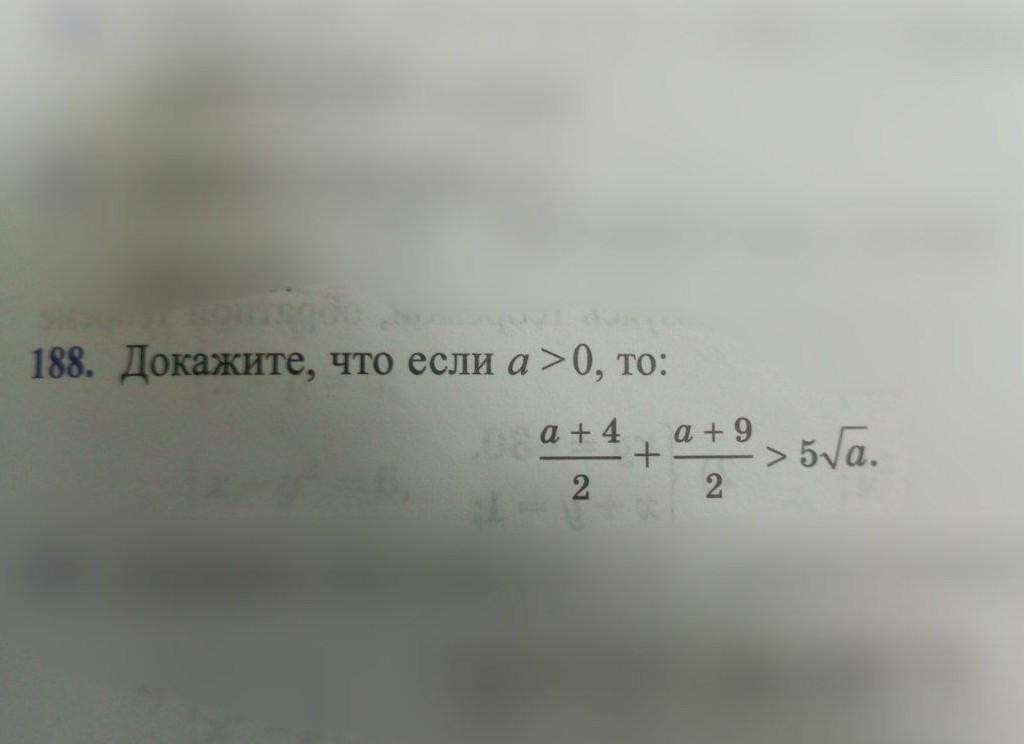
Ответы

Автор ответа: Ivan19074

Ответ:

Объяснение:

Пусть $b = \sqrt{a}$ , тогда получим:

$\frac{b^2 + 4}{2} + \frac{b^2 + 9}{2} > 5b\\b^2 + 4 + b^2 + 9 > 10b\\2b^2 + 13 > 10b\\2b^2 - 10b + 13 > 0\\b^2 - 5b + 6.5 > 0\\b^2 - 5b + 6.25 - 6.25 + 6.5 > 0\\(b - 2.5)^2 + 0.25 > 0\\$

Поскольку квадрат числа всегда положительный, неравенство будет всегда выполняться.

gulbahoraktamova40: спасибо

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Биология, автор: kobznina2

СРОЧНООО ДАЮ 15БАЛІВВ
опишіть серцевий цикл , особливості його фаз та їх тривалість

1 год назад

Предмет: Обществознание, автор: sarwskk

объясните почему значительная часть проблем возникающих жизни связаны с нормами права??????????

1 год назад

Предмет: Математика, автор: v4155127

5 1/4 : (х-1/3)=17/8

1 год назад

Предмет: Физика, автор: Anasteichenn

Срочно (Фізика 8 клас)

7 лет назад

Предмет: Алгебра, автор: ekatmar4enko2017

Выполни вычитание 2mm2−8m+16−6m−4.

7 лет назад

Докажите, что если а > 0, то: a + 4/2 + a + 9/2 > 5√адаю 15 баллов ​

Ответы

Докажите, что если а > 0, то: a + 4/2 + a + 9/2 > 5√а
даю 15 баллов