Предмет: Алгебра, автор: fctdgsygfdhngfxzgsac

Користуючись методом розкладу, обчислити інтеграли.

Приложения:

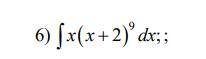
NNNLLL54: раскрывайте скобки по биному Ньютона

Ответы

Автор ответа: pushpull

1

Ответ:

в объяснении

Объяснение:

Формула разложения

$\displaystyle (a+b)^n=C_n^0a^nb^0+C_n^1a^{n-1}b^1+C_n^2a^{n-2}b^2+\; ...\; +C_n^na^0b^n$

в нашем случае

а - это х

b - это 2

n - это 9

Раскладываем скобку (х+2)⁹ и сразу умножаем каждый член разложения на х.

Получим

$\displaystyle x(x+2)^9 = x^{10}+18x^9+144x^8+672x^7+2016^x6+4032x^5+5376x^4+\\\\\\+4608x^3+2304x^2+512x$

И тогда наш интеграл распадается на сумму интегралов.

Записывать это очень долго, я напишу сразу проинтегрированный ответ

$\displaystyle \int x(x+2)^9 \;dx = \frac{x^{11}}{11} +\frac{9x^{10}}{5} +16x^9+84x^8+288x^7+672x^6+\\\\+\frac{5376x^5}{5} +1152x^4+768x^3+256x^2$

fctdgsygfdhngfxzgsac: спасибо большое))

pushpull: пожалуйста -))

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: Valeron2007

Помогите пожалуйста
Нужно ответить на вопросы!!
ДАЮ 100 БАЛЛОВ!!
1. Вы всегда ужинаете дома или иногда ходите куда-нибудь поесть?
2. Что вы обычно заказываете на основное блюдо (десерт)?
Что вы обычно пьешь?
3. Подаются ли национальные блюда в ресторанах?
4. Чем отличается обычный сервис от самообслуживания
ресторан? Что обычно дешевле?
5. Почему по всей стране закрылись многие кафе самообслуживания
настоящее время?

1 год назад

Предмет: Литература, автор: haliullinaskar37

составьте портрет Беликова (внешний и психологический) по рассказу А. П. Чехова "Человек в футляре"

1 год назад

Предмет: Математика, автор: syka8577

938. Запиши у вигляді дробу число: а) чотири сьомих; б) три десятих; в) сім восьмих.

1 год назад

Предмет: Другие предметы, автор: dariagrot

помогите пожалуйста срочно нужно буду заранее благодарна
надо написать конспект на тему возможности человека

7 лет назад

Предмет: Русский язык, автор: jarylgasnmalika

22.
Составьте определение понятия «Туризм», установив позицию: туризм - вид
спорта или вид путешествия. На данных вариантов выберите подходящий из них.
Kupuan
1) Туризм
- это физическая закалса организма, активный отдых,
досут, самообразование, познание, новые места, новые вершины.
2) Туристская среда вслючает в себя человека, природу, спорт, куль-
туру.
3) Туризм
выполняет познавательно-образовательную, воспита-
тельную, культурную, спортивно-оздоровительную функцию.

7 лет назад