В равнобедренном треугольнике ABC с основанием
AC проведена медиана BD . На сторонах AB и BC отмечены

точки E и F соответственно так, что AE=CF . Докажите, что

∠BED = ∠BFD .

Ответ:

Объяснение:

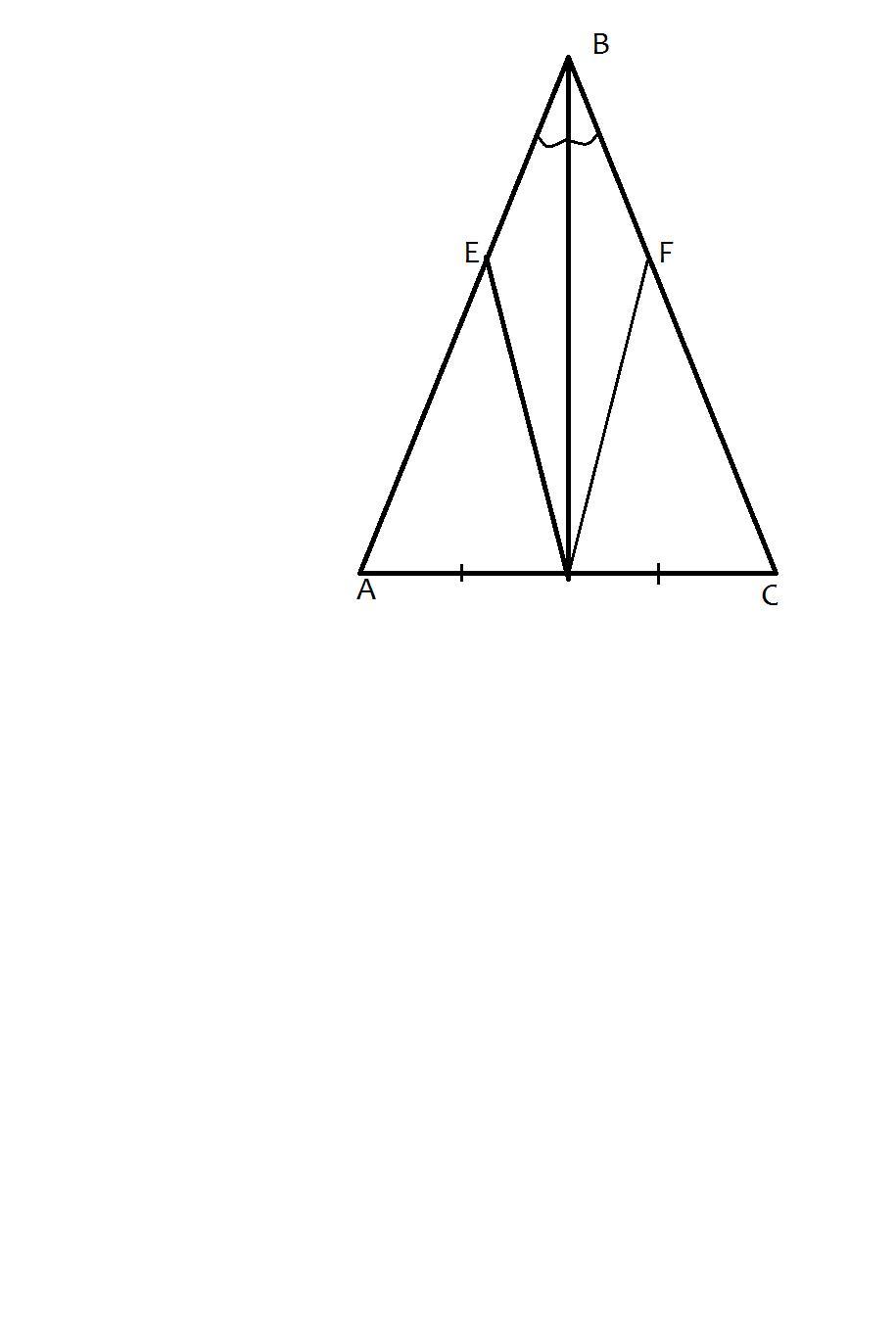
Дано: ΔАВС, АВ=ВС,  ВD - медиана, АЕ=СF. Доказать: ∠BED = ∠BFD .

АЕ=DF по условию, значит ВЕ=ВF;  ВD - общая сторона;  ∠ЕВD=∠FВDпо свойству медианы равнобедренного треугольника; ΔВЕD=ΔDFВ по первому признаку равенства треугольников, значит и ∠BED = ∠BFD . Доказано.