Предмет: Математика, автор: kardibalet

хелп ми плиззззззззз

Приложения:

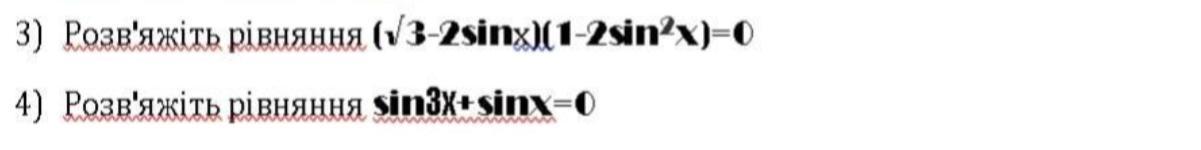
Ответы

Автор ответа: NNNLLL54

1

Ответ:

Тригонометрические уравнения .

Применяем формулу косинуса двойного угла .

$\bf 1)\ \ (\sqrt3-2sinx)(1-2sin^2x)=0$

Приравниваем каждый множитель к 0 .

$\displaystyle \bf a)\ \ \sqrt3-2sinx=0\ \ \to \ \ sinx=\frac{\sqrt3}{2}\ \ ,\\\\x=(-1)^{n}\cdot \frac{\pi }{3}+\pi n\ ,\ \ n\in Z\\\\b)\ \ 1-2sin^2x=0\ \ \to \ \ \ cos2x=0\ \ ,\\\\2x=\frac{\pi }{2}+\pi n\ \ ,\ \ \ x=\frac{\pi }{4}+\frac{\pi n}{2}\ \ ,\ \ n\in Z\\\\Otvet:\ x_1=(-1)^{n}\cdot \frac{\pi }{3}+\pi n\ ,\ x_2=\frac{\pi }{4}+\frac{\pi n}{2}\ \ ,\ \ n\in Z\ .$

Применяем формулу суммы синусов .

$\bf \displaystyle 2)\ \ sin3x+sinx=0\ \ \to \ \ \ 2\, sin2x\cdot cosx=0\\\\a)\ \ sin2x=0\ \ ,\ \ 2x=\pi n\ \ ,\ \ x=\frac{\pi n}{2}\ \ ,\ \ n\in Z\\\\b)\ \ cosx=0\ \ ,\ \ x=\frac{\pi }{2}+\pi k\ \ ,\ \ k\in Z$

Первую и вторую серии решений можно объединить в одну .

Ответ: $\bf x=\dfrac{\pi n}{2}\ \ ,\ \ n\in Z$ .

Приложения:

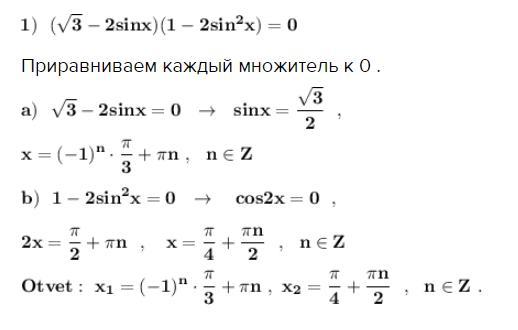
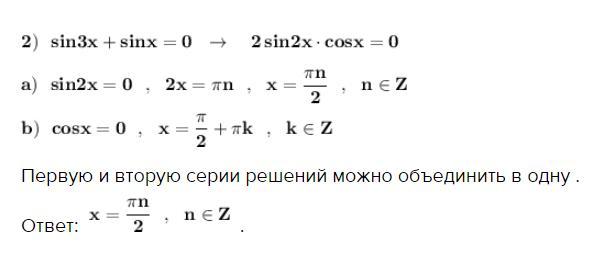
kardibalet: величайшее спасибо

kardibalet: https://znanija.com/task/54464117

kardibalet: такое еще есть

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Українська мова, автор: sorokavano40

ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО

1 год назад

Предмет: Математика, автор: gezalovasabina81

6 Mətndə yaşıl rəngdə verilmiş sözlərin əvəzinə aşağıdakılardan hansını işlətmək olar? Fikirlərinizi əsaslandırın. qarşılaşmaq, qorxutmaq, tutmaq, saxlamaq, vurmaq, toxundurmaq, keçmək, adlamaq, aşmaq, gözləri, baxışları, dayanmaq, söykənmək, təki, digər, zaman, gün а слова Rastlaşdı,yapışdı,döyəcləyərək,ötüb,nəzərləri,durmuşam,kimi,vaxtda.ПЖ СПАСИТЕ ЧЕРЕЗ 15 МИН В ШКОЛУ

1 год назад

Предмет: Українська мова, автор: alumnaeabseil0w

3. Виконайте завдання у форматі тесту ЗНО. 1. Чергування у -в без зміни значення слова можливе в усіх словах варіанта А утомитися, удень, уступ Г управа, удосконалення, уночі Д учитель, увійти, убогий Б уголос, уклад, уживати В увечері, удача, усередині 2. Правил чергування у -в дотримано у варіанті Г тайга, одягнена в хвою А в нашій країні Д у останньому вагоні Б збиратися в дорогу В навчалися у академії 3. Правил чергування у - в дотримано в усіх реченнях, ОКРІМ А Вірю я в правду свого ідеалу, Б Була весна, удень пригрівало сонце. В Яблуневі сади стояли вмиті росою. Г Яблуко м'яко скотилося у траву. Д Уже доспіли яблука, груші.

1 год назад

Предмет: Алгебра, автор: Leila95meow

1.101. Найдите все допустимые значения переменной:
1) √(4-x)^2

7 лет назад

Предмет: Математика, автор: Аноним

Решите СРОЧНО ПЛИЗ очень надоооо

7 лет назад