Предмет: Алгебра, автор: channeko

Знайди усі пари (x, y) дійсних чисел, які задовольняють рівняння

Приложения:

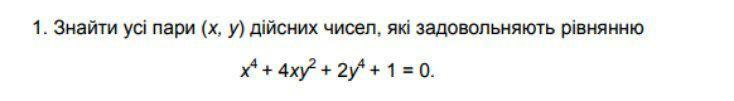
Ответы

Автор ответа: forqforq

Ответ:

Объяснение:

$x^4+4xy^2+2y^4+1=0\\y^2=t\geq 0\\x^4+4xt+2t^2+1=0\\2t^2+(4x)t+(x^4+1)=0\\D=16x^2-8x^4-8=-8(x^4-2x^2+1)=-8(x^2-1)^2$

$(x^2-1)^2\geq 0$ при умножении на отрицательное число даст отрицательный результат. Тогда нас устроит только случай D = 0:

$x^2-1=0\\x=+-1$

Рассмотрим каждый случай:

$1)\ x = 1:\\t=\frac{-4}{4}=-1\\y^2=-1\\\fbox{\text{no solution}}\\\\2)\ x = -1:\\t=\frac{4}{4}=1\\ y^2=1\\\fbox{y=+-1}$

Итого мы получаем две пары решений:

$(x,y)=(-1;1),(-1;-1)$

Интересные вопросы

Предмет: Физика, автор: v974921

1 год назад

Предмет: Қазақ тiлi, автор: ruslana1313Ari16

1 год назад

Предмет: Математика, автор: yasminchik2403

1 год назад

Предмет: Физика, автор: nozaninodilova2008

7 лет назад

Предмет: Алгебра, автор: Аноним

7 лет назад