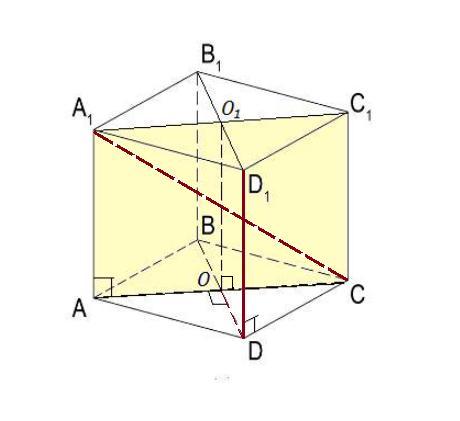
4. Дан куб АВСDA1B1C1D1 с ребром 4 см. Сделайте чертеж. Постройте общий перпендикуляр для скрещивающихся прямых А1С и DD1.Найдите расстояние между прямыми А1С и DD1.

Ответы
Ответ:
АВСD - куб с ребром равным 4 см .
Расстояние между скрещивающимися прямыми - это расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую прямую параллельно первой прямой .
А₁С лежит в плоскости АСС₁А₁ .
АА₁ || DD₁ (параллельны) как рёбра куба АА₁ лежит в плоскости ACC₁A₁ ⇒ плоскость АСС₁А₁ и прямая DD₁ параллельны :
DD₁ || пл. ACC₁A₁ .
Общий перпендикуляр будет перпендикулярен как DD₁ , так и пл. АСС₁А₁ . Причём его можно построить от любой точки ребра DD₁ к пл. АСС₁А₁ .
Им будет отрезок DO ( или D₁O₁ ) , лежащий в плоскости АВСD (или A₁В₁C₁D₁ ) , то есть DO ⊥ DD₁ и DO ⊥ ACC₁A₁ .
Так как все точки прямой DD₁ , параллельной плоскости АСС₁А₁ , находятся на одинаковом расстоянии от этой плоскости, искомое расстояние равно DO .
ABCD - квадрат. Диагонали квадрата пересекаются под прямым углом и точкой пересечения делятся пополам.
∆ АОD равнобедренный прямоугольный треугольник . Его острые углы равны 45° .
DO = АD • sin45° = 4 • √2/2 = 2√2 (см)