Предмет: Алгебра, автор: rokfeller007

Задание уровня С3 !!
во вложении...

Приложения:

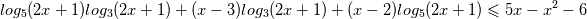
Ответы

Автор ответа: Матов
0
log_{5}(2x+1)*log_{3}(2x+1)+(x-3)log_{3}(2x+1)+(x-2)log_{5}(2x+1) leq 5x-x^2-6
5x-x^2-6=(3-x)(x-2)
Откуда получим 
 (log_{5}(2x+1)+x-3)(log_{3}(2x+1)+x-2) leq 0 \ x>-0.5\\
   1) left { {{log_{5}(2x+1)+x-3 leq 0} atop {log_{3}(2x+1)+x-2 geq 0}} right. \\ 2)left { {{ log_{5}(2x+1)+x-3 geq 0} atop { log_{3}(2x+1)+x-2 leq 0}} right. \\ 1)\ 2x+1 leq 5^{3-x}\ 2x+1 geq 3^{2-x}\ 2)\ 2x+1 geq 5^{3-x}\ 2x+1 leq 3^{2-x}\\
 
Очевидно что равенство достигается при x=2   в первом , и  x=1   во втором , строя  графики  решение первой будет 
(-oo;2] ;[1;+oo) по частям 
и во втором   [2;+oo)\ (-oo;1]  
Учитывая ОДЗ получим ответ 
  [1;2]
 


Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Математика, автор: musalliyalim58
Решите уравнение: Т+(-754)=(-754)+(+450)​
6 лет назад
Предмет: Русский язык, автор: grhddhdrtf
сочинение рассуждение родная природа в 3 абзаца​
6 лет назад
Предмет: Українська мова, автор: chocorice242
у якому відмінку іменники вживаються тільки з прийменником?
1)у родовому
2)у давальному
3)у місцевому
4)у кличному
5)у знахідному ​
6 лет назад
Предмет: Алгебра, автор: taniyjla

Пусть f(x+3)=x в квадрате + 4x + 5. Найти f(x)
10 лет назад
Предмет: Биология, автор: lenura12

4)Большинство растений семейство розоцветных имеют цветок из 4 чашелистиков ,5 лепестков ,5 тычинок ,пестиков —много или один ,плод -яблоко ,костянка или сборный орешек.Исправь ошибки в перечисленных признаках

 

 

 

5)Какие особенности строения цветка бобовых растений7Каких представителей этого семейства ты знаешь?
10 лет назад