Предмет: Математика, автор: AntonTimoshin

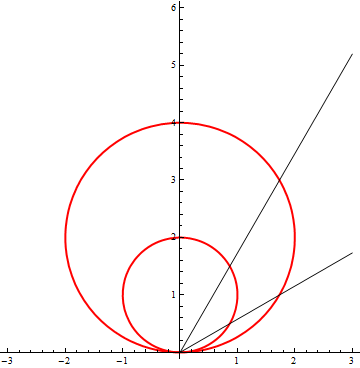
Найти площадь области D. Рисунок вроде составил, а вот с продолжением проблеммы, заранее спасибо.

Приложения:

Ответы

Автор ответа: nomathpls

Первая окружность: $x^2+(y-1)^2=1$ с центром в $(0;1)$ и радиусом $1$
Вторая окружность: $x^2+(y-2)^2=4$ с центром в $(0;2)$ и радиусом $2$

Чуть повнимательнее. У меня такие же проблемы были, но потом рука привыкла.

А потом проинтегрировать в полярных координатах: полюс в начале координат, полярная ось направлена в положительную сторону оси X. Большую окружность представим в виде $r=4sintheta$ , а маленькую - $r=2sintheta$ . Две прямые соответствуют уравнениям $alpha=30^o$ и $beta=60^o$ . Площадь, заключенная между двумя прямыми (задаваемыми углами $theta$ ) и полярной функцией, заданной уравнением $r=f(theta)$ , вычисляется следующим образом:

$S=frac{1}{2} intlimits^beta_alpha {r^2} , dtheta$

Дальше все ясно: найдем кусок площади большого круга и вычтем из него кусок площади маленького.

$S_1=frac{1}{2} intlimits^{pi /3}_{pi/6} {(2sintheta)^2} , dtheta=2intlimits^{pi /3}_{pi/6} {sin^2theta} , dtheta=2(frac{theta}{2}-frac{1}{4}sin(2theta)|^{pi/3}_{pi/6})= \ =(theta-frac{1}{2}sin(2theta))|^{pi/3}_{pi/6}=(frac{pi}{3}-frac{sqrt{3}}{4})-(frac{pi}{6}-frac{sqrt{3}}{4})=frac{pi}{6}$

Площадь большого куска находится аналогично, она будет отличаться от найденной в 4 раза (там выносится 16 из под интеграла после возведения функции в квадрат). $S_2=frac{2pi}{3}$ .

Итак, $S=S_2-S_1=frac{pi}{2}$

Приложения:

Автор ответа: AntonTimoshin

огромное спасибо, болел, пропустил эту тему, а через 30 минут контрольная, огромное спасибо)

Автор ответа: AntonTimoshin

не понимаю данную замену на r*sin, но думаю разберусь, ере раз спасибо)

Автор ответа: AntonTimoshin

теперь все понял, решил совершенно другой вариант, схема ясна, огромнейшее спасибо

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Биология, автор: kseniahoroseva376

помогите пж даю 20 баллов срочно!!!!!!

6 лет назад

Предмет: Биология, автор: rostikb1260

характеристика видів РНК і ДНК (не порівняння)

6 лет назад

Предмет: Физика, автор: vitalikk012

Помогите решить задачу пожалуйста, очень срочно!

6 лет назад

Предмет: Биология, автор: mashar1

Два типа клеток ( живые зеленые и мертвые водоносные) характерны для... 1. кукушкиного льна 2.сфагнума 3. щитовника мужского 4. сосны обыкновенной

10 лет назад

Предмет: Геометрия, автор: vitek6

В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2, а прилежащий угол равен 30°. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°. Найдите объем цилиндра.

10 лет назад