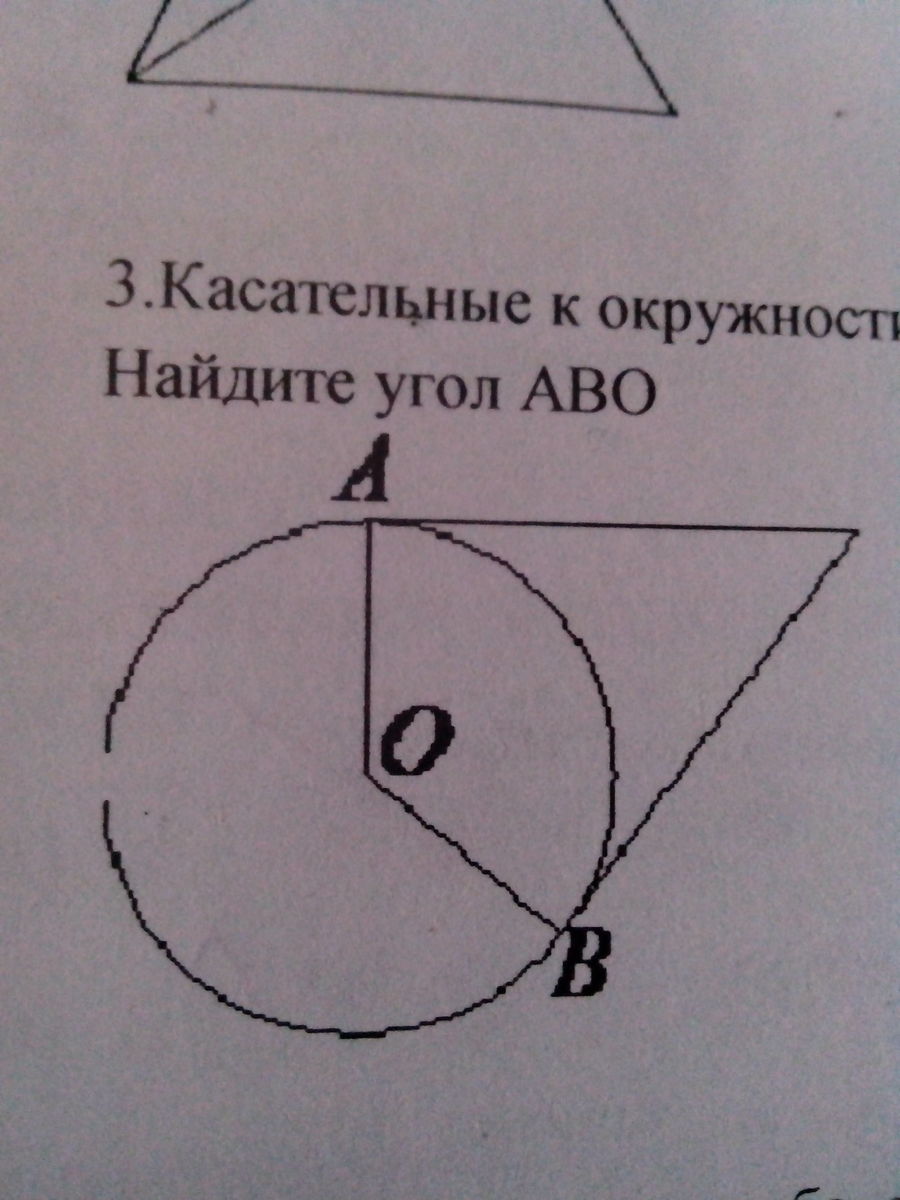
Касательные к окружности с центром O в точках A и B пересекаются под углом 12 градусов. Найдите угол ABO.

 Угол ОАС = углу OВС = 90(т.к. радиус перпендикулярен к касательной) и угол АСВ = 12
Тогда угол АОВ = 360 - (90 + 90 + 12) = 168.
Треугольник АОВ равнобедренный(ОВ = ОА - радиусы), значит углы при основании равны. 180 - 168 = 12(угол АВО + угол ОАВ), значит угол АВО = 6