Предмет: Геометрия,
автор: crysisww
Докажите, что основание равнобедренного треугольника параллельно биссектрисе одного из внешних углов.
Приложения:
Ответы
Автор ответа:
0
Дано:
ΔABC - равнобедренный, BC - основание
AH - биссектриса ∠CAD
Доказать: BC ║ AH
∠CAD = ∠ABC + ∠ACB (по теореме о внешнем угле треугольника)
∠ABC = ∠ACB ⇒ ∠CAD = 2∠ACB
Биссектриса делит угол пополам, следовательно ∠DAH = ∠CAH = ∠ACB
∠CAH = ∠ACB, AC - секущая для прямых AH и BC ⇒ AH ║BC так как их накрест лежащие углы(∠CAH и ∠ACB) равны
Приложения:
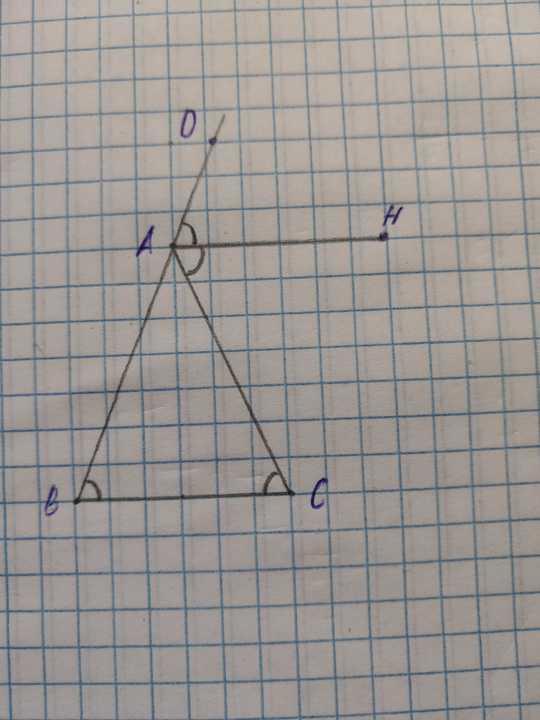
Интересные вопросы
Предмет: Математика,
автор: 12juliashal12
Предмет: Биология,
автор: 198122221
Предмет: География,
автор: aAlena43
Предмет: Алгебра,
автор: 123569