СРОЧНО! ПОМОГИТЕ ПОЖАЛУЙСТА!! Может хотя бы одну решите..плиииз!

1.В прямом параллелепипеде ABCDA1B1C1D1 основанием служит параллелограмм ABCD, AD=2, , <A=30 градусов. б0льшая диагональ составляет с плоскостью основания угол 45 градусов. Найдите площадь боковой поверхности параллелепипеда.

 2. Основанием пирамиды MABC служат прямоугольный треугольник ABC, катеты которого AC=8 см, BC=6 см. Высота пирамиды равна  см. Двугранные углы при основании пирамиды равны между собой. Найдите площадь полной поверхности пирамиды. 

3. В укозанном выше параллелепипеде найдите угол между A1C и плоскостью грани DD1C1C.

 Сразу говорю, в интернете решения ни одной из этих задач нет. Помогите пожалуйста, мне очень надо...((

 

 

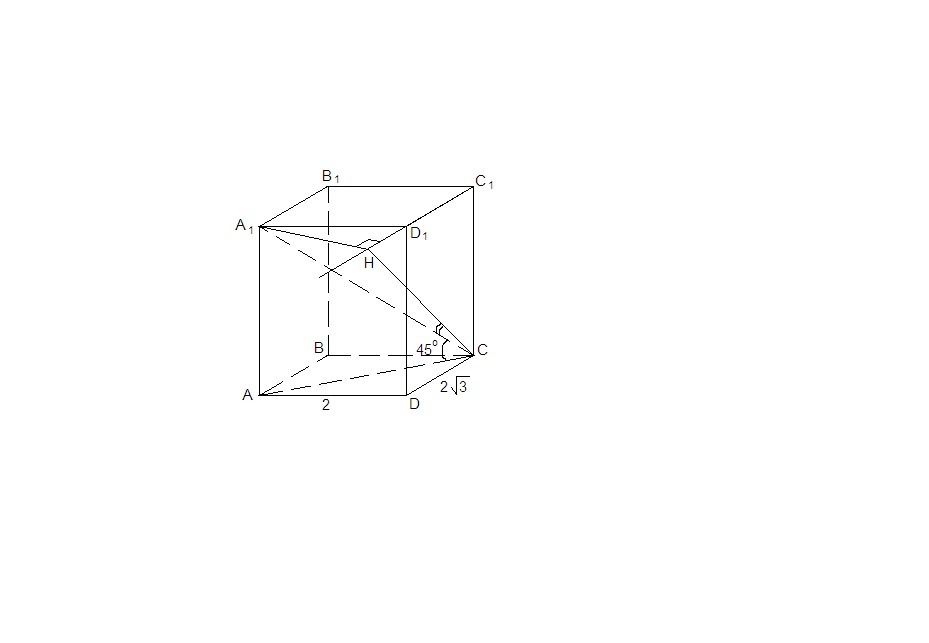
1.
Большей будет диагональ, соединяющая вершины острых углов оснований.
Ребро AA₁ перпендикулярно плоскости основания. Значит, АС проекция A₁С на плоскость основания. ⇒∠A₁СА = 45°.
ΔADC: AD = 2, DC = 2√3, ∠ADC = 180° - 30° = 150° (сумма углов параллелограмма, прилежащих к одной стороне 180°). По теореме косинусов:
AC = √(AD² + DC² - 2AD·DC·cos150°) =
      = √(4 + 12 + 2·2·2√3·√3/2) = √(16 +12) = √28 = 2√7
ΔA₁СА: ∠A₁AC = 90°, ∠A₁СА = 45°, ⇒ ∠CA₁А = 45°, т.е. треугольник равнобедренный, A₁А = АС = 2√7
Sбок = Pосн · A₁А = (2 + 2√3)·2 · 2√7 = 8√7·(1 + √3)

3.
Проведем A₁H⊥D₁C₁. DD₁⊥(A₁B₁C₁)⇒DD₁⊥A₁H ⇒A₁H⊥(D₁C₁C)
Тогда НС - проекция A₁C на плоскость (D₁C₁C). ∠ A₁СH искомый.
ΔA₁СА: ∠A₁AC = 90°, по теореме Пифагора
               A₁C = √(АС² + АА₁²) = √(28 + 28) = 2√14
Sabcd = AD·DC·sin150° = 2·2√3·1/2 = 2√3
Sabcd = DC·A₁H
2√3 = 2√3 · A₁H
A₁H = 1
ΔA₁HC: ∠A₁HC = 90°,
               sin∠A₁СH = AH/A₁C = 1/(2√14) = √14/28

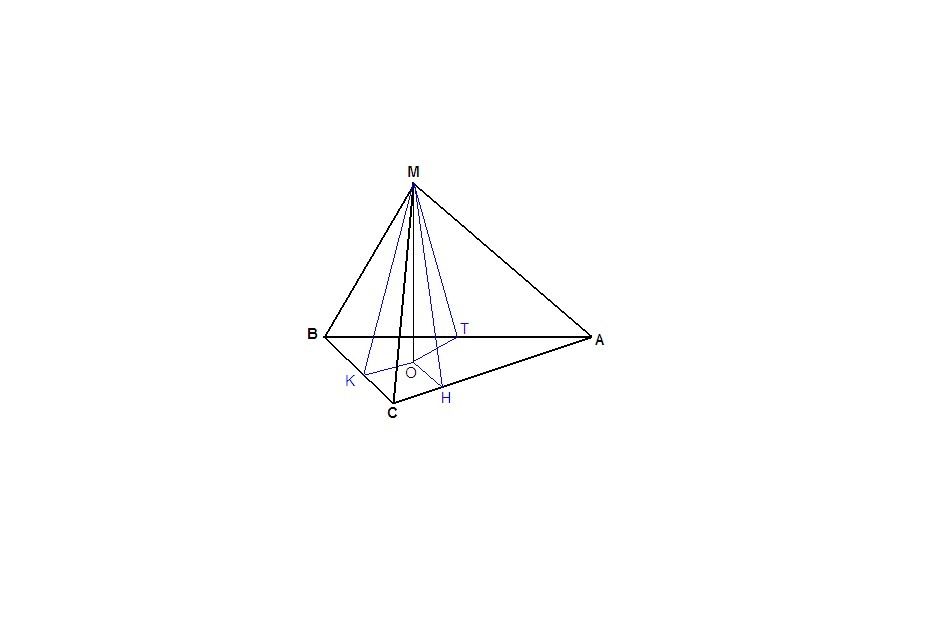
2.
Пусть О - основание высоты пирамиды. Проведем из точки О перпендикуляры ОТ, ОН и ОК к ребрам основания. Тогда ОТ, ОН и ОК проекции наклонных МТ, МН и МК на плоскость основания. Значит, и МТ, МН и МК перпендикулярны соответствующим ребрам основания.
⇒ ∠МТО =∠МКО = ∠МНО - линейные углы двугранных углов при основании.
⇒ ΔМТО =ΔМКО = ΔМНО по катету (МО общий) и противолежащему острому углу.
⇒ О - центр окружности, вписанной в основание.

ΔАВС: ∠С = 90°, по теореме Пифагора
             АВ = √(ВС² + АС²) = √(36 + 64) = 10
r = p - c, где r - радиус окружности, вписанной в основание, р - его полупериметр, с -гипотенуза.
r = (10 + 8 + 6)/2 - 10 = 2
ΔMOH: ∠MOH = 90°, по теореме Пифагора
               MH = √(MO² + OH²) = √(45 + 4) = 7
MH = MK = MT ⇒
Sбок = Pосн/2 · MH = 12 · 7 = 84 см²
Sосн = AC·CB/2 = 24 см²
Sполн = Sбок + Sосн = 84 + 24 = 108 см²