Докажите что , если медиана треугольника равна половине стороны , к которой она проведена , то треугольник прямоугольный.

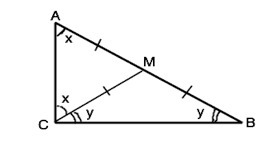
Пусть в ∆ АВС отрезок СМ - медиана и по условию СМ=АМ=ВМ. Тогда ∆ АМС и ∆ ВМС - равнобедренные с равными углами при основаниях. Примем ∠МАС=∠МСА=х, и ∠МСВ=МВС =у

Сумма углов треугольника 180° ⇒ 2х+2у=180° ⇒ х+у=90°. Тогда ∠АСВ=х+у=90°. ⇒ ∆ АВС - прямоугольный. Доказано.