Предмет: Геометрия,
автор: oksanapolyakovа
Касательные к окружности с центром О в точках А и В пересекаются под углом 72 градуса. Найдите угол АВО. Ответ дайте в градусах.
Приложения:
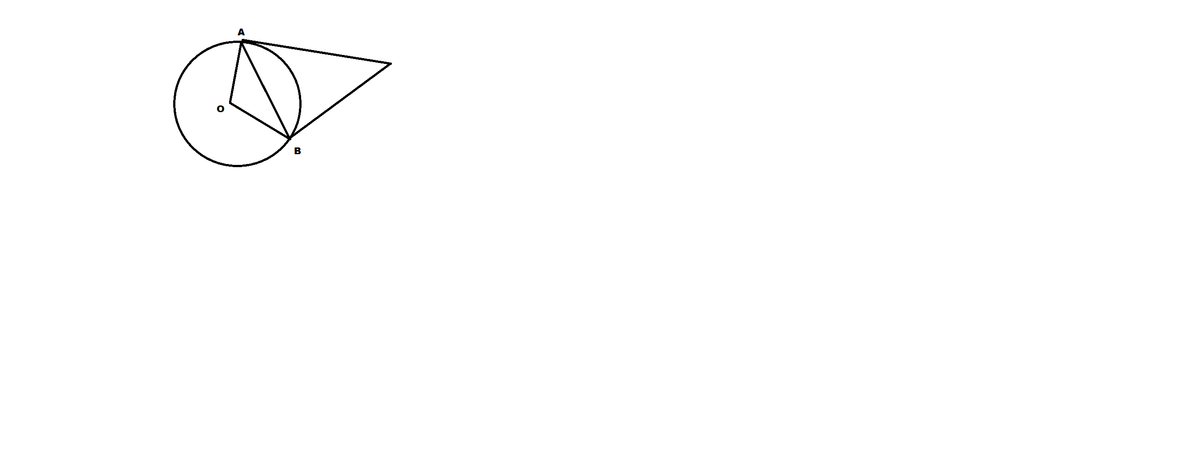
Ответы
Автор ответа:
0
Точку пересечения касательных обозначим К
Угол АКВ=72 град
Угол КАО=углу КВО=90 градусов. Касательная перпендикулярна радиусу в точке касания
В четырехугольнике КАОВ сумма всех углов 360 градусов. Значит угол АОВ= 108 град
Угол ВАО=углу АВО=72/2= 36 градусов
Угол АКВ=72 град
Угол КАО=углу КВО=90 градусов. Касательная перпендикулярна радиусу в точке касания
В четырехугольнике КАОВ сумма всех углов 360 градусов. Значит угол АОВ= 108 град
Угол ВАО=углу АВО=72/2= 36 градусов
Автор ответа:
0
может быть 180??
Автор ответа:
0
Ответ верный. угол АОВ = 108, потому что угол АКВ=72 градуса (это дано: точка К - точка пересечения касательных). Да в ответе все объяснено...
Автор ответа:
0
Так что решение правильное
Интересные вопросы
Предмет: Математика,
автор: kislovin
Предмет: Другие предметы,
автор: amirsurov020111
Предмет: Химия,
автор: dimakurakun07
Предмет: Математика,
автор: pogoda007
Предмет: Обществознание,
автор: wwwceit