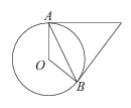
Касательные к окружности с центром  O  в точках  A  и  B  пересекаются под углом  72 градуса. Найдите угол ABO. Ответ дайте  в градусах. 

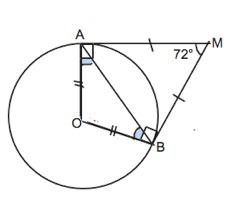
 Обозначим точку пересечения данных касательных М 

а) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. 

б) Отрезки касательных к окружности, проведенных из одной точки, равны. ⇒ 

∆ АМВ равнобедренный (АМ=ВМ). 

∆ АОВ равнобедренный (АО=ВО)

Сумма углов четырехугольника 360°. ∠МАО=∠МВО=90°⇒

∠АОВ=360°-2•90°-72°=108°

∠А=∠В=(180°-108}):2=36°