Помогите решить.Срочно.
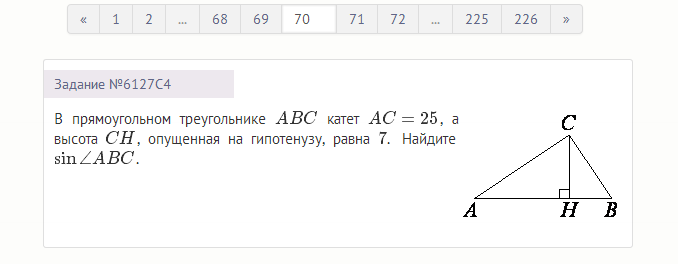
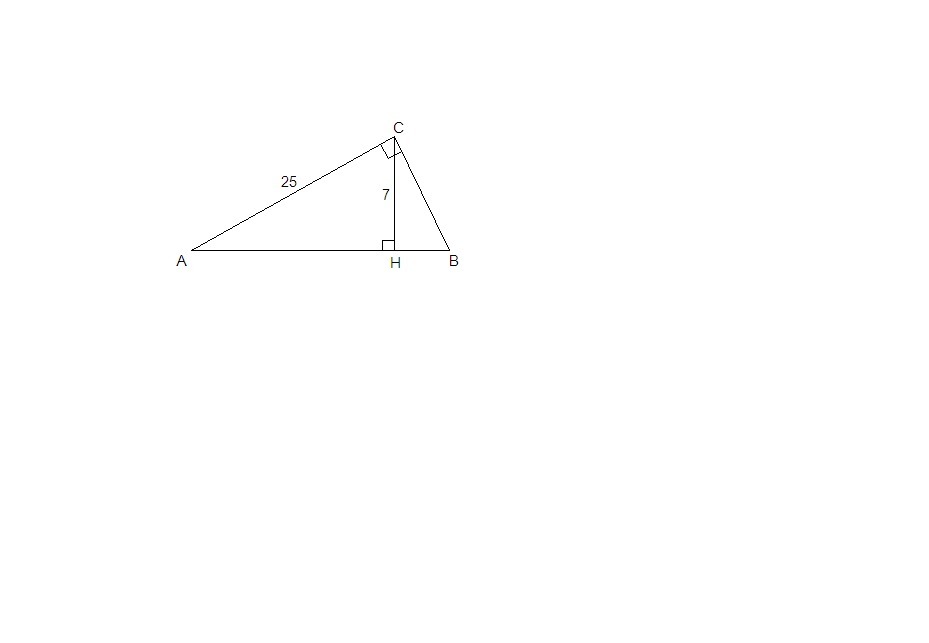
В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 7. Найдите sin∠ABC.

В ΔАСН:
∠Н = 90°, sin∠CAH = CH/AC = 7/25

Сумма острых углов прямоугольного треугольника ABC равна 90°, поэтому
∠CAB = 90° - ∠ABC
sin∠CAH =  sin (90° - ∠ABC) = cos∠ABC
sin∠ABC = √(1 - cos²∠ABC) = √(1 - 49/625) = √((625 - 49)/625) = 24/25