Серединные перпендикуляры к сторонам ABи CDчетырехугольника ABCD пересекаются на стороне AD. Докажите, что если углы Aи Dчетырехугольника ABCD равны, то его диагонали ACи BD также равны.

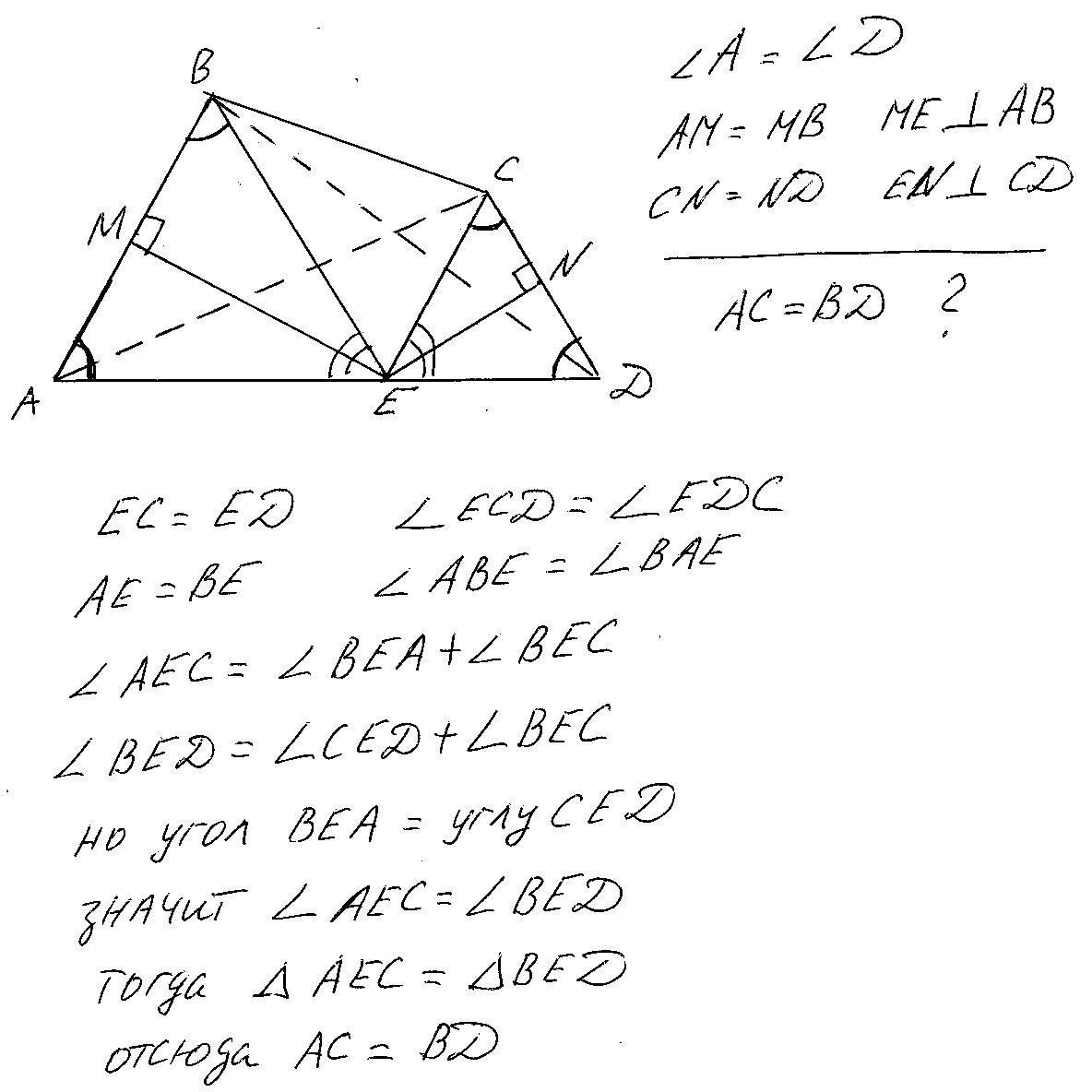
Проведём из вершины С прямую СЕ, из вершины В прямую ВЕ(смотри рисунок). Поскольку СN=NД и ЕN перпендикуляр к СД, то треугольник СЕД равнобедренный и ЕС =ЕД. Аналогично АЕ=ВЕ. Отсюда равны углы ВЕА и СЕД. Далее рассматриваем треугольники АЕС и ВЕД. Они равны по двум сторонам и углу между ними, следовательно против равных углов у них лежат равные стороны и АС=ВД.