Предмет: Математика,
автор: yokii
Фигура, ограниченная гиперболой x^2-y^2=1 и прямой x=2 вращается вокруг оси абсцисс. Найти объем тела вращения.
Ответы
Автор ответа:
0
Выразим 
с 
Точки пересечения
![sqrt{1+y^2}=2\
1+y^2=4\
y=+-sqrt{3}](https://tex.z-dn.net/?f=sqrt%7B1%2By%5E2%7D%3D2%5C%0A+1%2By%5E2%3D4%5C%0A+y%3D%2B-sqrt%7B3%7D "sqrt{1+y^2}=2\
1+y^2=4\
y=+-sqrt{3}")
По формуле
Ответ
Точки пересечения
По формуле
Ответ
Автор ответа:
0
x²-y²=1
y²=x²-1
Точки пересечения с осью х
у=0
x²-1=0
x²=1
x₁=-1
x₂=1
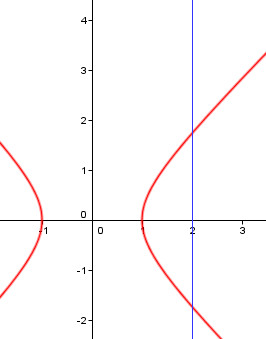
Делаем чертеж
![V= pi intlimits^2_1 f^2{(x}) , dx = pi intlimits^2_1 (x^2-1)} , dx= pi ( frac{x^3}{3} -x)|_1^2= \
=pi ( frac{2^3}{3} -2- frac{1^3}{3}+1)=pi ( frac{8}{3}- frac{1}{3}-1)= frac{4}{3} pi](https://tex.z-dn.net/?f=V%3D+pi++intlimits%5E2_1+f%5E2%7B%28x%7D%29+%2C+dx+%3D+pi++intlimits%5E2_1+%28x%5E2-1%29%7D+%2C+dx%3D+pi+%28+frac%7Bx%5E3%7D%7B3%7D+-x%29%7C_1%5E2%3D+%5C+%0A%3Dpi+%28+frac%7B2%5E3%7D%7B3%7D+-2-+frac%7B1%5E3%7D%7B3%7D%2B1%29%3Dpi+%28+frac%7B8%7D%7B3%7D-+frac%7B1%7D%7B3%7D-1%29%3D+frac%7B4%7D%7B3%7D+pi+ "V= pi intlimits^2_1 f^2{(x}) , dx = pi intlimits^2_1 (x^2-1)} , dx= pi ( frac{x^3}{3} -x)|_1^2= \
=pi ( frac{2^3}{3} -2- frac{1^3}{3}+1)=pi ( frac{8}{3}- frac{1}{3}-1)= frac{4}{3} pi")
y²=x²-1
Точки пересечения с осью х
у=0
x²-1=0
x²=1
x₁=-1
x₂=1
Делаем чертеж
Приложения:
Интересные вопросы