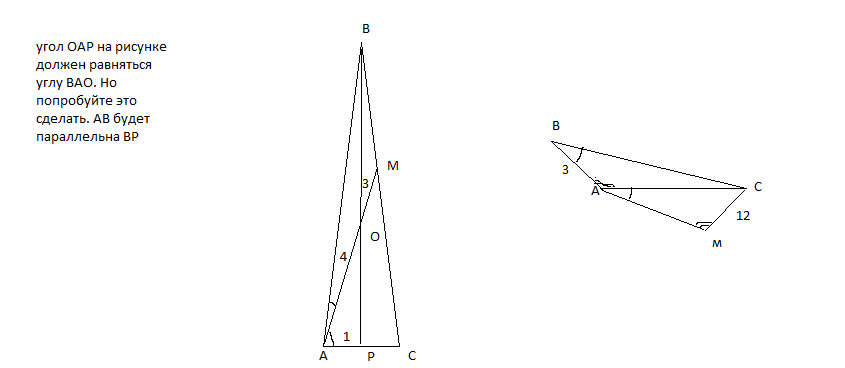
1.В равнобедренном треугольнике АВС с основанием АС высота ВР и биссектриса АМ пересекаются в точке О, АО=4, ОМ=3,АС=2. Найдите боковую сторону треугольника АВС.
2.Точки В и М лежат по разные стороны от прямой АС, угол АВС = углу САМ, угол ВАС= углу АМС, АВ=3, СМ=12. Найдите длину отрезка АС

1) Неправильное условие.
Треугольник АОР: прямоугольный, АО=4, АР=1 ( так как треугольник АВС равнобедренный и ВР является и высотой и медианой АР=РС)
Значит, по теореме Пифагора  ОР=√15. Найдем tgα=ОР/АР=√15, где α=<OAP
Но АМ-биссектриса, значит угол ВАС=2α



Получается, что угол А - тупой. Чего быть не может в равнобедренном треугольнике.
2) треугольники АВс и АМС подобны по двум углам.
Значит,
 


k- коэффициент подобия.
Тогда АМ=3k, AC=12/k, ВС=АС/k=12/k²
Недостаточно данных для нахождения к.

Это ведь не черчение, здесь не спрашивается можно построить или нет. Нужен алгоритм нахождения боковой стороны