Предмет: Алгебра,
автор: msgula1970
Используя формулы сложных корней,
упростите выражение:
Приложения:
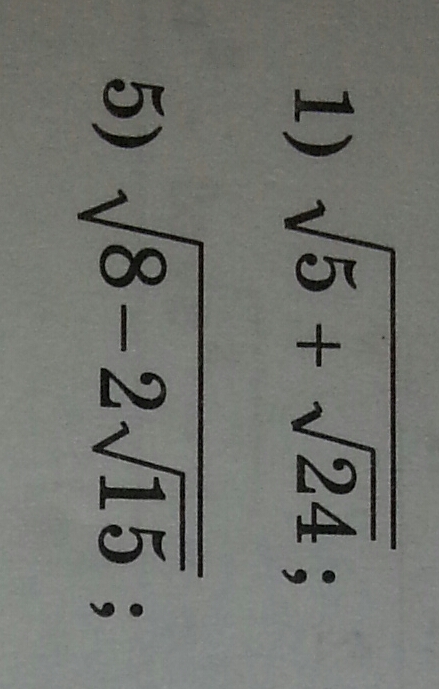
Ответы
Автор ответа:
0
На мой взгляд, эта формула нужна для тех случаев, когда получающиеся выражения будут чуть посложнее, чем тут. Очевидно же, что
5 + sqrt(24) = 5 + 2sqrt(6) = (sqrt(3) + sqrt(2))^2
8 - 2sqrt(15) = (sqrt(5) - sqrt(3))^2,
так что в ответе будет sqrt(3) + sqrt(2) и sqrt(5) - sqrt(3).
Я, честно говоря, эту формулу никогда не запоминала ввиду того, что её проще вывести, чем запомнить. Это можно проделать, например, так:
пусть A +- sqrt(B) = (x +- y)^2, причем x^2 + y^2 = A, 4x^2 y^2 = B. По теореме Виета x^2, y^2 - корни уравнения t^2 - At + B/4 = 0, т.е. x, y = (A +- sqrt(A^2 - B))/2. Выбирая x > y > 0, получаем
A +- sqrt(B) = (sqrt((A + sqrt(A^2 - B))/2) +- sqrt((A - sqrt(A^2 - B))/2))^2
sqrt(A +- sqrt(B)) = sqrt((A + sqrt(A^2 - B))/2) +- sqrt((A - sqrt(A^2 - B))/2)
По факту почти всегда легче угадать ответ.
5 + sqrt(24) = 5 + 2sqrt(6) = (sqrt(3) + sqrt(2))^2
8 - 2sqrt(15) = (sqrt(5) - sqrt(3))^2,
так что в ответе будет sqrt(3) + sqrt(2) и sqrt(5) - sqrt(3).
Я, честно говоря, эту формулу никогда не запоминала ввиду того, что её проще вывести, чем запомнить. Это можно проделать, например, так:
пусть A +- sqrt(B) = (x +- y)^2, причем x^2 + y^2 = A, 4x^2 y^2 = B. По теореме Виета x^2, y^2 - корни уравнения t^2 - At + B/4 = 0, т.е. x, y = (A +- sqrt(A^2 - B))/2. Выбирая x > y > 0, получаем
A +- sqrt(B) = (sqrt((A + sqrt(A^2 - B))/2) +- sqrt((A - sqrt(A^2 - B))/2))^2
sqrt(A +- sqrt(B)) = sqrt((A + sqrt(A^2 - B))/2) +- sqrt((A - sqrt(A^2 - B))/2)
По факту почти всегда легче угадать ответ.
Интересные вопросы
Предмет: Другие предметы,
автор: Nnnddd1819
Предмет: Русский язык,
автор: yanabalchenkova
Предмет: Другие предметы,
автор: kimdzenni732
Предмет: История,
автор: FUKS003200
Предмет: Математика,
автор: babyyou