Я совсем наглая, но всё ещё прошу вашей помощи!
Докажите, что биссектриса угла А треугольника АВС проходит через точку пересечения прямых, содержащих биссектрисы внешних углов при вершинах В и С.

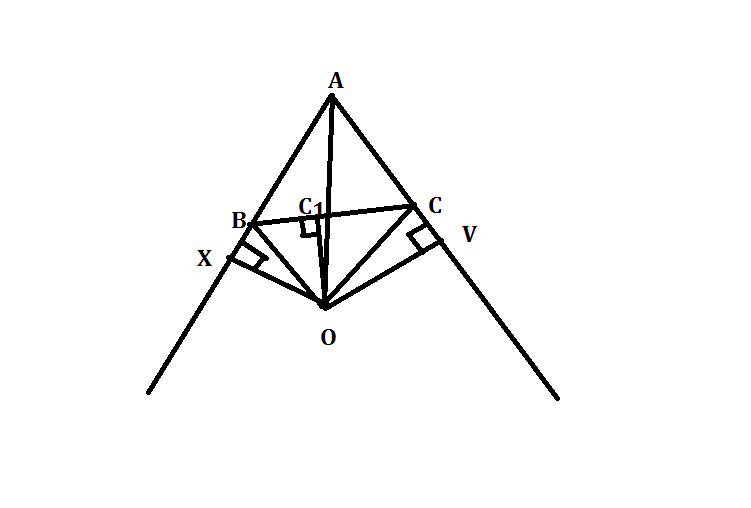
Опустим перпендикуляры OX OV OC1.
Углы  XBO=OBС1  тк   углы X=C1=90.  ТО и углы XOB=BOC1 (в соображениях  суммы углов треугольника)
ТО треугольники   XOB и BOC1  равны   по  стороне и  2 прилежащим углам. То  OX=OC1. Ну  и в  силу симметрии  рассуждений по той же причине  равны треугольники  OC1C и  OCV .  OC1=OV
Но  тогда выходит  что: OX=OV.
Откуда прямоугольные  треугольники  XOA и VOA равны  по катету и общей гипотенузе  AO. 
То  углы: XAO=VAO. ТО есть  AO-биссектриса угла A.  Другими  словами биссектриса  угла A проходит через точку пересечения  биссектрис  других внешних углов.
ЧТД