Исследование функции y=1/(1+x^2) Помогите пожалуйста.
и найдите функцию обратную данной.

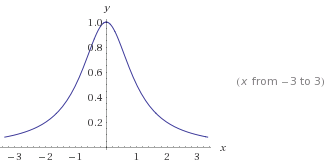
область определения - все числа (знаменатель всегда положителен)
область значений - от 0 до 1
нули функции отсутствуют

находим производную:

производная равна нулю в точке х = 0
функция возрастает на промежутке от минус бесконечности до нуля
функция убывает на промежутке от нуля до плюс бесконечности

горизонтальная асимптота y=0

график приложен

у=1/(1+х²)
х=1/(1+у²)
1+у²=1/х
у²=1/х - 1=(1-х)/х
-обратная функция