Предмет: Геометрия,
автор: Anasteiha
Докажите что если у параллелограмма диагональ делит угол на две равные части, то он является ромбом.
Ответы
Автор ответа:
0
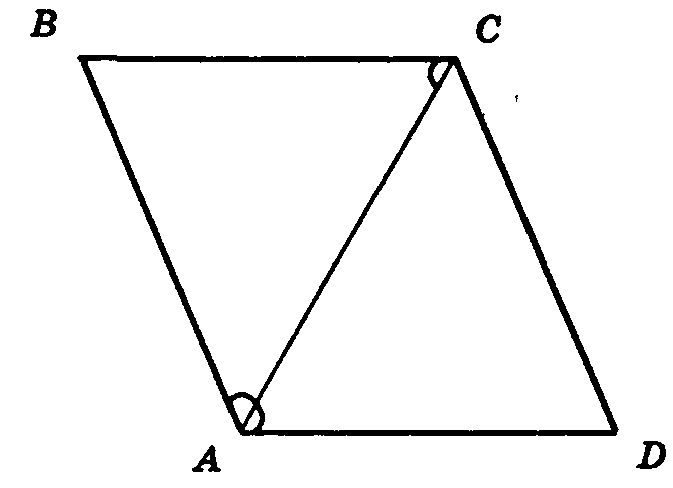
Смотри вложение.
Пусть АС биссектриса и диагональ в параллелограмме ABCD
тогда<BAC=<CAD, <BCA=<CAD
(как накрест лежащие углы для параллельных ВС и AD и секущей АС). Тогда,<BAC=<BCA
а значит треугольник ABC
равнобедренный с основанием AC
Значит, AB=BC
По свойству параллелограмма
AB=CD,BC=AD
как противоположные стороны. Итак, все стороны параллелограмма ABCD равны, значит, он ромб. Что и требовалось доказать.
Приложения:
Интересные вопросы