Предмет: Алгебра,
автор: porsh711
300 баллов. Решите уравнение и неравенство.
Приложения:
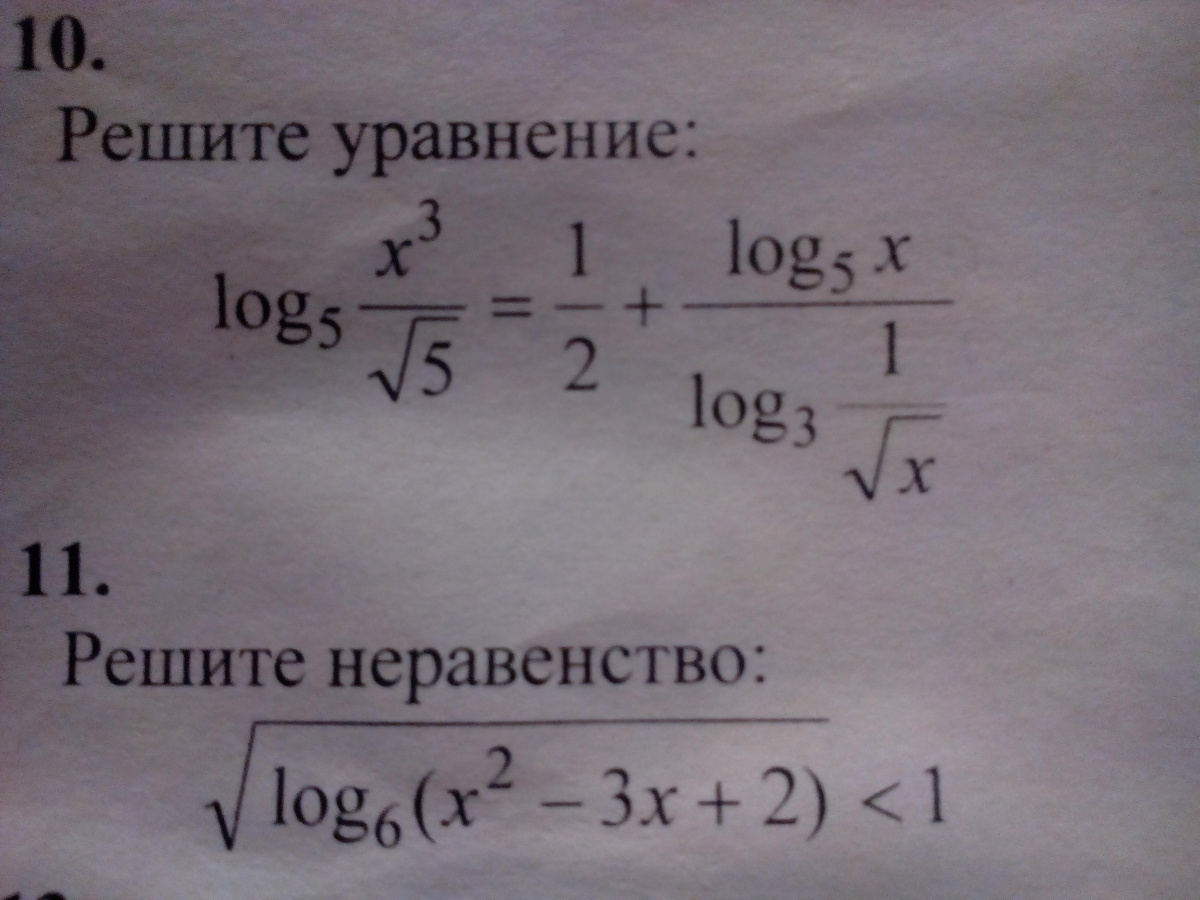
Ответы
Автор ответа:
0
10)3log(5)x - 1/2=1/2 +log(5)x :(-1/2log(5)x :log(5)3)
3log(5)x - 1/2=1/2+log(5)x *(-2log(5)3 :log(5)x
3log(5)x=1-2log(5)3
3log(5)x=log(5)5/9
log(5)x=log(5)![sqrt[3]{5/9} sqrt[3]{5/9}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B5%2F9%7D+)
x=![sqrt[3]{5/9} sqrt[3]{5/9}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B5%2F9%7D+)
11)ОДЗ
x²-3x+2≥0 U log(6)(x²-3x+2)≥0
x²-3x+2≥0
x1+x2=3 U x1*x2=2⇒x1=1 U x2=2⇒x≤1 U x≥2
log(6)(x²-3x+2)≥0
x²-3x+2≥1
x²-3x+1≥0
D=9-4=5
x1=(3-√5)/2 U x2=(3+√5)/2⇒x≤(3-√5)/2 U x≥(3+√5)/2
x∈(-∞;(3-√5)/2] U [(3+√5)/2;∞)
log(6)(x²-3x+2)<1
x²-3x+2<6
x²-3x-4<0
x1+x2=3 U x1*x2=-4⇒x1=-1 U x2=4⇒-1<x<4
x≤(3-√5)/2 U x≥(3+√5)/2 U -1<x<4⇒x∈(-1;(3-√5)/2 ] U [((3+√5)/2 ;4)
3log(5)x - 1/2=1/2+log(5)x *(-2log(5)3 :log(5)x
3log(5)x=1-2log(5)3
3log(5)x=log(5)5/9
log(5)x=log(5)
x=
11)ОДЗ
x²-3x+2≥0 U log(6)(x²-3x+2)≥0
x²-3x+2≥0
x1+x2=3 U x1*x2=2⇒x1=1 U x2=2⇒x≤1 U x≥2
log(6)(x²-3x+2)≥0
x²-3x+2≥1
x²-3x+1≥0
D=9-4=5
x1=(3-√5)/2 U x2=(3+√5)/2⇒x≤(3-√5)/2 U x≥(3+√5)/2
x∈(-∞;(3-√5)/2] U [(3+√5)/2;∞)
log(6)(x²-3x+2)<1
x²-3x+2<6
x²-3x-4<0
x1+x2=3 U x1*x2=-4⇒x1=-1 U x2=4⇒-1<x<4
x≤(3-√5)/2 U x≥(3+√5)/2 U -1<x<4⇒x∈(-1;(3-√5)/2 ] U [((3+√5)/2 ;4)
Интересные вопросы
Предмет: Физика,
автор: naskoval07
Предмет: Математика,
автор: aneldilmukhan
Предмет: Українська мова,
автор: Аноним
Предмет: Алгебра,
автор: Аноним