Предмет: Алгебра,
автор: ксюнечка73829129
24.9
Помогите , пожалуйста :з
Приложения:
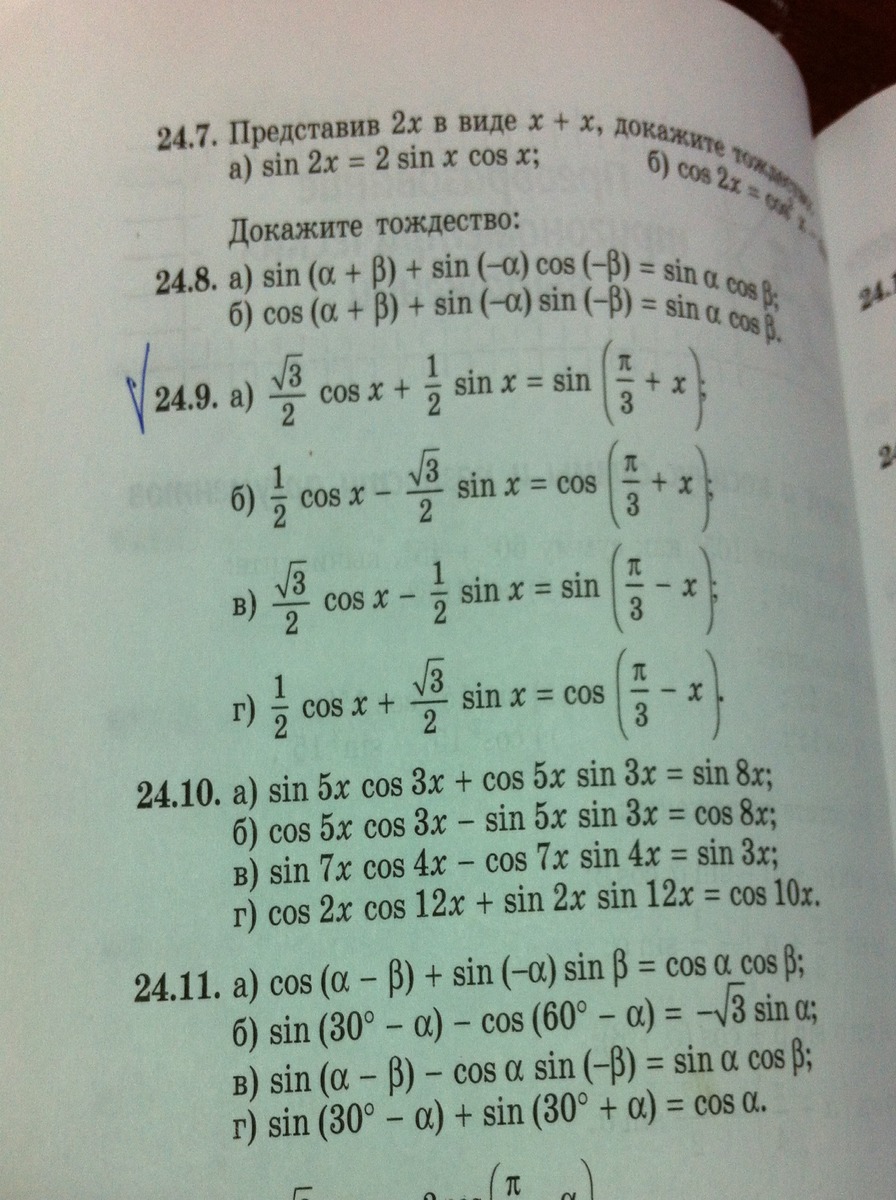
Ответы
Автор ответа:
0
Решение
Учитывая, что sin(π/3) = √3/2; cos(π/3) = 1/2 и применяя формулы сложения и вычитания, получаем:
1) sin(π/3)*sinx + cos(π/3)*cosx = sin(π/3 + x)
2) cos(π/3)*cosx - sin(π/3)*sinx = cos(π/3 + x)
3) sin(π/3)*cosx - cos(π/3)*sinx = sin(π/3 - x)
4) cos(π/3)*cosx + sin(π/3)*sinx = cos(π/3 - x)
Учитывая, что sin(π/3) = √3/2; cos(π/3) = 1/2 и применяя формулы сложения и вычитания, получаем:
1) sin(π/3)*sinx + cos(π/3)*cosx = sin(π/3 + x)
2) cos(π/3)*cosx - sin(π/3)*sinx = cos(π/3 + x)
3) sin(π/3)*cosx - cos(π/3)*sinx = sin(π/3 - x)
4) cos(π/3)*cosx + sin(π/3)*sinx = cos(π/3 - x)
Интересные вопросы
Предмет: Математика,
автор: DIMOOOOOON15
Предмет: Химия,
автор: lashkaravaana1
Предмет: Қазақ тiлi,
автор: nursultanzhomartuly
Предмет: Математика,
автор: lavrenyukmarin