Предмет: Алгебра, автор: Аноним

Найдите значение выражения sin(arccos 4/5-arccos 3/5)

Ответы

Автор ответа: Anastsiia

0

$sin(arccos 4/5-arccos 3/5)=sin(arccos 4/5)cos(arccos 3/5)- \ -cos(arccos 4/5)sin(arccos 3/5)= >\ \ sin(arccos 4/5)= sqrt{1-cos^2(arccos 4/5)}= sqrt{1-16/25}= sqrt{9/25}=3/5 \ cos(arccos 3/5)=3/5 \ cos(arccos 4/5)= 4/5 \ sin(arccos 3/5)= sqrt{1-cos^2(arccos 3/5)}= sqrt{1-9/25}= sqrt{16/25}=4/5 \ \ => = 3/5*3/5-4/5*4/5=9/25-16/25=-7/25$

Приложения:

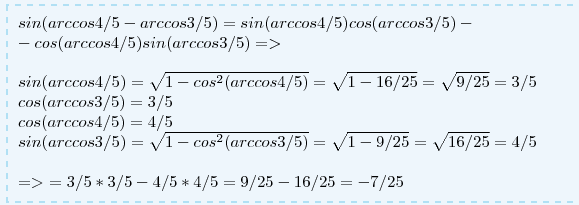
Автор ответа: Аноним

0

СпасибО!!!

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Кыргыз тили, автор: straiker132222

156. текстти окугала. этиштерди көчуруп жазып чактаркын анык тагыла.

6 лет назад

Предмет: Қазақ тiлi, автор: gulyaali1970

54. Сөздерді оқып, әрқайсысының тұсына қысқарған түрін жаз.
Біріккен Ұлттар Ұйымы, Америка Құрама Штаттары,
Ұлттық ғылым академиясы, Тәуелсіз Мемлекеттер Дос-
тастығы.
Үлгі: Біріккен Ұлттар Ұйымы БҰҰ.

6 лет назад

Предмет: Химия, автор: nurievazhibek

а) 2Na + O2 = Na2O2

Реагенты: натрий и кислород

б) Образуется - пероксид натрия (Na2O2)

с) При взаимодействии натрия с кислородом образуется пероксид натрия

6 лет назад

Предмет: Алгебра, автор: аленёнок

авиабилет для взрослого стоит 11400 рублей. стоимость билета для школьника составляет 35 % от стоимости билета для взрослого. Группа состоит из 10 школьников и 2 взрослых. Сколько стоят билеты на всю группу?

10 лет назад

Предмет: Математика, автор: Аноним

Объясните тему:Нахождение дроби от числа.

10 лет назад