Предмет: Геометрия,
автор: Гексли
Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30 градусов меньше другого
Ответы
Автор ответа:
0
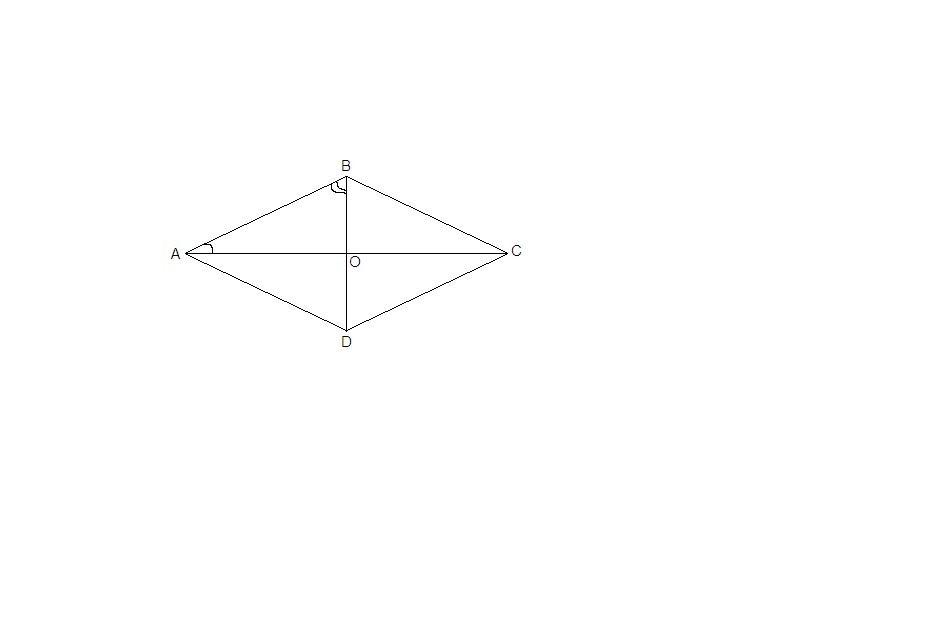
Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.
ΔАОВ: ∠АОВ = 90°, ∠АВО - ∠ВАО = 30°
но ∠АВО + ∠ВАО = 90° т.к. сумма острых углов прямоугольного треугольника равна 90°.
Получаем ∠АВО = (90° + 30°) /2 = 60°, значит ∠ВАО = 90° - 60° = 30°.
В ромбе ∠А = ∠С = 2ВАО = 60°
∠В = ∠D = 2∠АВО = 120°
ΔАОВ: ∠АОВ = 90°, ∠АВО - ∠ВАО = 30°
но ∠АВО + ∠ВАО = 90° т.к. сумма острых углов прямоугольного треугольника равна 90°.
Получаем ∠АВО = (90° + 30°) /2 = 60°, значит ∠ВАО = 90° - 60° = 30°.
В ромбе ∠А = ∠С = 2ВАО = 60°
∠В = ∠D = 2∠АВО = 120°
Приложения:
Интересные вопросы
Предмет: Алгебра,
автор: Nikita56645654556788
Предмет: Математика,
автор: tanyasivobrova
Предмет: Алгебра,
автор: egor8780
Предмет: Химия,
автор: khdj