Предмет: Алгебра, автор: Krekerss

1. Найти интеграл методом почленного интегрирования

Приложения:

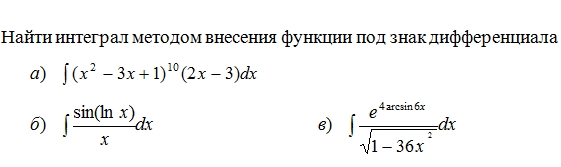
Ответы

Автор ответа: dtnth

0

$int {frac {x^{frac{1}{3}}x^3}{6}-frac {sin 3x}{2}+frac{5}{x}} , dx = int {frac {x^{frac{1}{3}}x^3}{6} ,dx- int frac {sin 3x}{2} , dx +int frac{5}{x}} , dx=$

$frac {1}{6}int {{x^{frac{10}{3}} ,dx-frac{1}{2} int {sin 3x} , dx+ 5int frac{1}{x}} , dx=$

$frac{1}{6}frac {x^frac{13}{3}}{frac{13}{3}}-frac{1}{2} frac{1}{3}cos (3x)+5ln|x|+C= frac{1}{26}{x^frac{13}{3}}-frac{1}{6}cos (3x)+5ln|x|+C$ , c є R

$int{frac {6x^2+x^4-x^{frac{1}{2}}}{x}}, dx=int{6x+x^3-x^{frac{-1}{2}}, dx= int{6x, dx+int x^3, dx-int x^{frac{-1}{2}}, dx=$

$6int{x, dx+int x^3, dx-int x^{frac{-1}{2}}, dx= 6frac {x^2}{2} +frac{x^4}{4}-frac{x^frac{1}{2}}{frac{1}{2}}+c=$

$3x^2 +frac{x^4}{4}-2x^frac{1}{2}}+c$ ,c є R

$int{frac{2x}{x^3+x}-3e^x+frac{5x^2}{3x^3}}, dx= int{frac{2}{x^2+1}-3e^x+frac{5}{3x}}, dx= int{frac{2}{x^2+1}, dx-int3e^x, dx+intfrac{5}{3x}}, dx= 2int{frac{1}{x^2+1}, dx-3inte^x, dx+frac{5}{3}intfrac{1}{x}}, dx= 2arctg(x) -3e^x+frac{5}{3}ln|x|+c$ ,c є R

картинка ведь одна была???

$int{(x^2-3x+1)^{10} (2x-3)}, dx=$

$int{(x^2-3x+1)^{10}}, d(x^2-3x+1)= frac{(x^2-3x+1)^{11}}{11}+c$ ,c є R

$int{ frac {sin (ln x)}{x}}, dx=int{ frac {sin (ln x)}, d ln x=-cos (ln x)+c$ ,c є R

$int{frac {e^{4arcsin 6x}}{sqrt{1-36x^2}}}, dx= frac {1}{24}int{{e^{4arcsin 6x}}, d(4arcsin 6x)= frac {1}{24} e^{4arcsin 6x} + c$ ,c є R

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Қазақ тiлi, автор: erkezansugaeva7

адамды сұлу ететін не нәрсе?

7 лет назад

Предмет: Русский язык, автор: Аноним

206.

Спеши, вставляя пропущенные согласные.Обрати внимание:в каком слове ты слышишь непроиносимые согласныезвук.

7 лет назад

Предмет: Математика, автор: skintpep

запишите дроби вида 7-а/а+2 в порядке возрастания, если а =1, 2, 3, 4, 5, 6.

7 лет назад

Предмет: Математика, автор: Лесялиса

Сколько натуральных чисел расположено между чмслами 27 и 83? И какие тоже напишите...

10 лет назад

Предмет: Алгебра, автор: Олександр14

Знайдіть швидкість і довжину поїзда, якщо він проходить уздовж платформи завдовжки 378 м за 25 с., а повз нерухомого пасажира - за 7 с.

10 лет назад